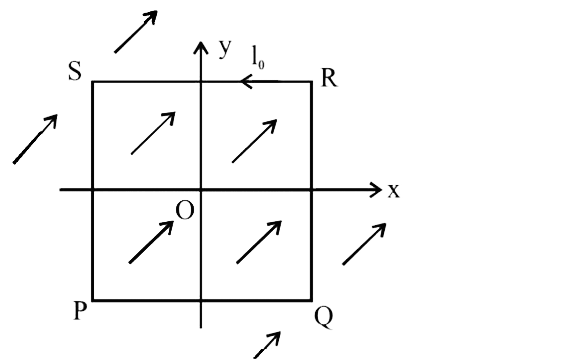
A uniform constant magnetic field B is directed at an angle of 45∘ to the x-axis in the xy plane. PQRS is a rigid square wire frame carrying a steady current I (clockwise), with its center at the origin O. At time t = 0, the frame is at rest in the position shown in fig. With its sides parallel to the x and y axes. Each side of the frame is of mass M and length L.
Find the initial angular acceleration of the frame. Assume that the frame is in a gravity free space free from any other influence.

(1) To find the angular acceleration of the frame, we need to know the moment of inertia of the frame for which we further need to know the axis about which the frame is rotating. Now, this can be a little trickly because as per the information given, the frame is not hinged at any point. We know that the force on a magnetic dipole in a uniform magnetic field is zero. So, the torque that we have calculated is actually a couple. So, whatever be the axis of rotation, the torque will turn out to be the same.
(2) Since there is no net force, the center of mass of the body should be at rest. So, the frame should rotate about its center of mass.
(3) The torque vector is in the direction of the axis of rotation. So, this means that the frame is rotating about an axis in the xy plane about its diagonal. We can use the perpendicular axis theorem to find the angular acceleration.
Calculations : Using perpendicular axis theorem we can say that
I1+I2=IZ,
where I1 and I2 are the moments of inertia of the frame about the diagonals. Also, by symmetry, I1=I2.
By parallel axis theorem, the moment of inertia of each of the rods about the z axis is given by
ML212+M(L2)2=ML23.
So, the moment of inertia of the entire frame about the z axis is given by
Iz=4ML23
But we can say that
I1=Iz2=2ML23
By using the expression τ=I1α, we get
α=τI1=iL2B2ML2/3=3iB2M
Topper's Solved these Questions
- MAGNETIC FORCEBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Check point
6 Videos
- MAGNETIC FORCEBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Problems
49 Videos
- MAGNETIC FIELDS DUE TO CURRENTSBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)
4 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )
3 Videos
Similar Questions
A uniform constant magnetic field B is directed at an angle of 45∘ to the xaξs in the xy- plane . PQRS is a rigid, square wire frame carrying a steady current I0, with its centre at the origin O. At time t=0, the frame is at rest in the position as shown in figure , with its sides parallel to the xandy axis. Each side of the frame is of mass M and length L.
(a) What is the torque τ about O acting on the frame due to the magnetic field?
(b) Find the angle by which the frame rotates under the action of this torque in a short interval of time Δt, and the axis about this rotation occurs .(Δtissoshorttˆanyvariation∈the→rquedur∈gthis∫ervalmaybe¬≤cted.)Given:themomentof∫eriaoftheameaboutanaξsthroughitscentreperpendica––r→itsaboutanaξsthroughitscentreperpendica––r→itspla≠is(4)/(3) ML^(2).
View SolutionA uniform constant magnetic field B is directed at an angle of 45∘ to the xaξs in the xy- plane . PQRS is a rigid, square wire frame carrying a steady current I0, with its centre at the origin O. At time t=0, the frame is at rest in the position as shown in figure , with its sides parallel to the xandy axis. Each side of the frame is of mass M and length L.
(a) What is the torque τ about O acting on the frame due to the magnetic field?
(b) Find the angle by which the frame rotates under the action of this torque in a short interval of time Δt, and the axis about this rotation occurs .(Δtissoshorttˆanyvariation∈the→rquedur∈gthis∫ervalmaybe¬≤cted.)Given:themomentof∫eriaoftheameaboutanaξsthroughitscentreperpendica––r→itsaboutanaξsthroughitscentreperpendica––r→itspla≠is(4)/(3) ML^(2).

View Solution
Knowledge Check
A long wire carrying current I is connected to a rectangular metallic frame as shown in the adjacent figure. A uniform magnetic field B along y-axis is switched on. The mass linear density of the frame is λ. The frame lies in y-z plane, The instantaneous angular acceleration of the frame is
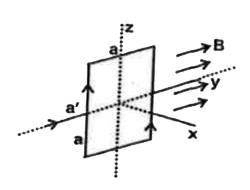 AzeroB12lBλaC4lBλaDnone of the above
AzeroB12lBλaC4lBλaDnone of the aboveFour identical rods each of mass m and length l are joined to form a rigid square frame. The frame lies in the xy plane, with its centre at the origin and the sides parallel to the x and y axes. Its moment of inertial about
Athe x-axis is (2/3)ml2Bthe z-axi is (43)ml2Can axis parallel to the z-axis and passing through a corner is (10/3)ml2Done side is (5/2)ml2Four identical rods each of mass m and length l are joined to form a rigid square frame. The frame lies in the xy plane, with its centre at the origin and the sides parallel to the x and y axes. Its moment of inertial about
Athe x-axis is 23ml2Bthe z-axis is 43ml2Can axis parallel to the z-axis and passing through a corner is 103ml2Done side is 53ml2
A long wire carrying current I is connected to a rectangular metallic frame as shown in the adjacent figure. A uniform magnetic field B along y-axis is switched on. The mass linear density of the frame is λ. The frame lies in y-z plane, The instantaneous angular acceleration of the frame is

View SolutionFour identical rods each of mass m and length l are joined to form a rigid square frame. The frame lies in the xy plane, with its centre at the origin and the sides parallel to the x and y axes. Its moment of inertia about
View SolutionAn equilateral triangular frame with side a carrying a current I is placed at a distance a from an infinitely long straight wire carrying a current I as shown in the figure. One side of the frame isparallel to the wire. The whole system lies in the xy-plane. Find the magnetic force F acting on the frame.
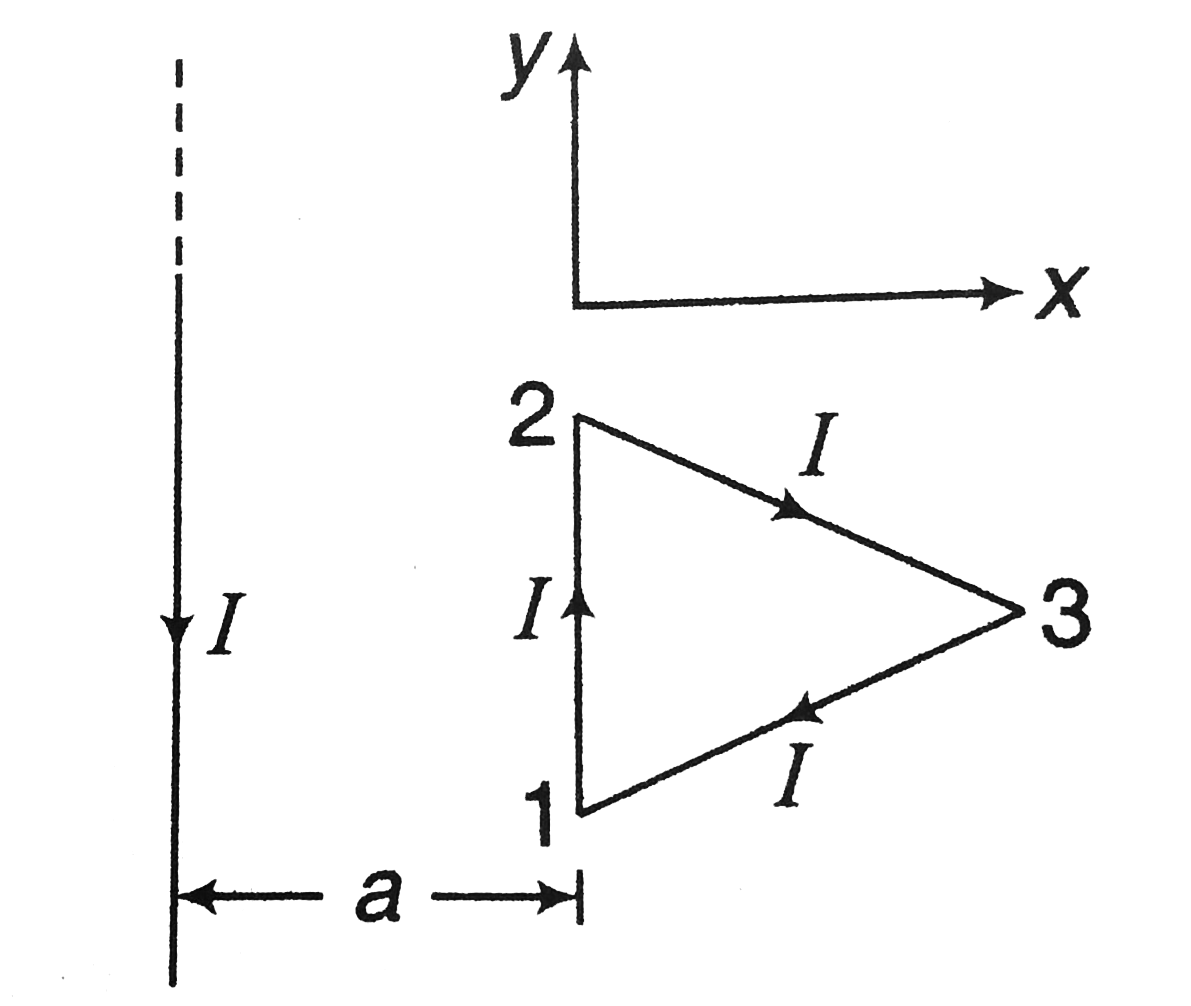
View SolutionAn equilateral triangular frame with side a carrying a current I is placed at a distance a from an infinitely long straight wire carrying a current I as shown in the figure. One side of the frame isparallel to the wire. The whole system lies in the xy-plane. Find the magnetic force F acting on the frame.

View SolutionA current of 2 A enters at the corner d of a square frame abcd of side 20 cm and leaves at the opposite corner b. A magnetic field B= 0.1 T exists in the space in a direction perpendicular to the plane of the frame as shown in Find the magnitude and direction of the magnetic forces on the four sides of the frame.

View Solution
