A plank of mass m is lying on a rough suface having coeffient of frinction as μ is situation as shown in fig Find the acceleration of the plank assuming that it slips and the surface of body exposed to radiaton is black body.
KEY IDEA
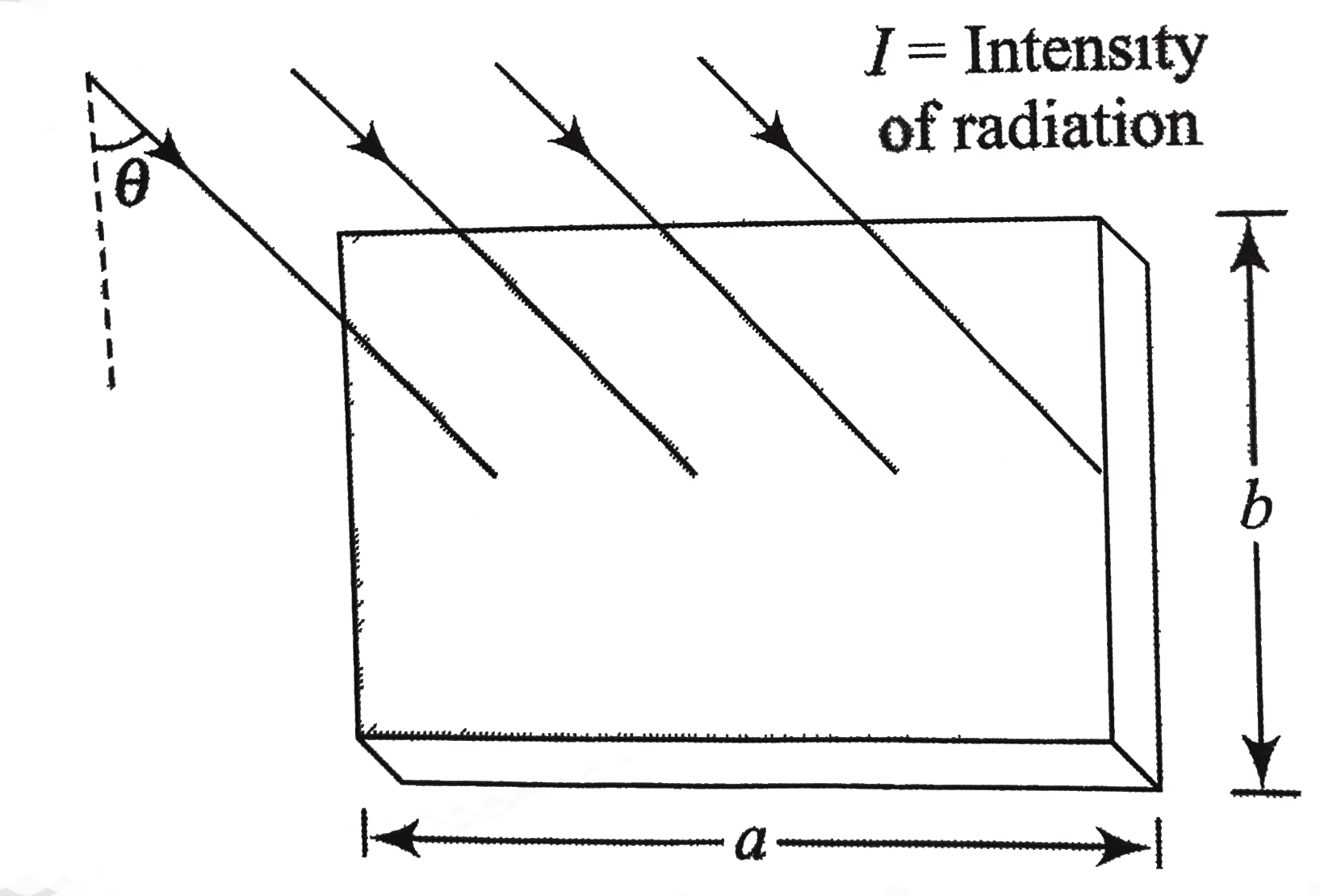
First of all let us find the energy received per second by surface exposed to radiation. The area of the surface is ab. But the area of across section of the beam incident on the surface is not ab. From the figure, the area of cross section of the beam is ab cosθ.
Calculation : So, the power of the incident beam is
P=Iabcosθ
The number of photons incident per unit time can be found by
P=dndt×hcλ
So,
dndt=Iabcosθλhc

A light beam incident on a black body at an angle θ to the normal.
Each of the photon will be completely absorbed by the surface. This will produce an impulse in the normal direction will be absorbed by the surface on which it is kept.
Radiation force experience by surface is
F=dndt×p
where p is the momentum of the photon incident. By de Broglie.s hypothesis,
p=hλ,
F=Iabcosθc
Topper's Solved these Questions
- PHOTONS AND MATTER WAVESBOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - Check points
3 Videos
- PHOTONS AND MATTER WAVESBOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PROBLEMS
50 Videos
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions
57 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
Similar Questions
Knowledge Check
A body of mass m is placed on a rough surface with coefficient of friction μ inclined at θ. If the mass is in equilibrium , then
Aθ=tan−1μBθ=tan−1(1μ)Cθ=tan−1(m)μDθ=tan−1(μ)mA body of mass m slides down a rough plane of inclination α . If μ is the coefficient of friction, then acceleration of the body will be
AgsinαBμcosαCg(sinα−μcosα)Dg(cosα−μsinα)A block of mass m lying on a rough horizontal surface of friction coefficient μ is pulled by a force F as shown , the limiting friction between the block and surface will be
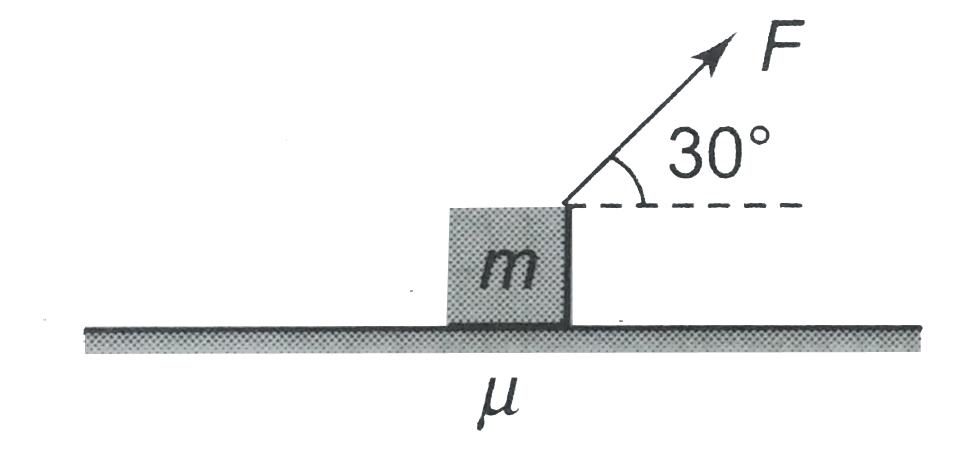 AμmgBμ(mg+F2)Cμ(mg−F2)Dμ(mg−√3F2)
AμmgBμ(mg+F2)Cμ(mg−F2)Dμ(mg−√3F2)
A plank of mass M is placed on a rough horizontal force F is applied on it A man of mass m rens on the plank find the acceleration of the man so that the plank does not move on the surface . The coefficent of friction between the plank and the surface is μ Assume that the man does not slip on the plank

View SolutionA plank of mass M is placed on a rough horizontal surface and a contant horizontal force F is applied on it . A man of mass m runs on the plank find the range of acceleration of the man that the plank does not move on the surface is μ .Assume that the does not slip on the plank

View Solution
Consider a cylinder of mass M and radius R lying on a rough horizontal plane. It has a plank lying on its top as shown in figure. A force F is applied on the plank such that the plank moves and causes the cylinder to roll the plank always remains horizontal. there is no slipping at any point of contact. Calculate the acceleration of the cylinder and the frictional forces at the two contact.
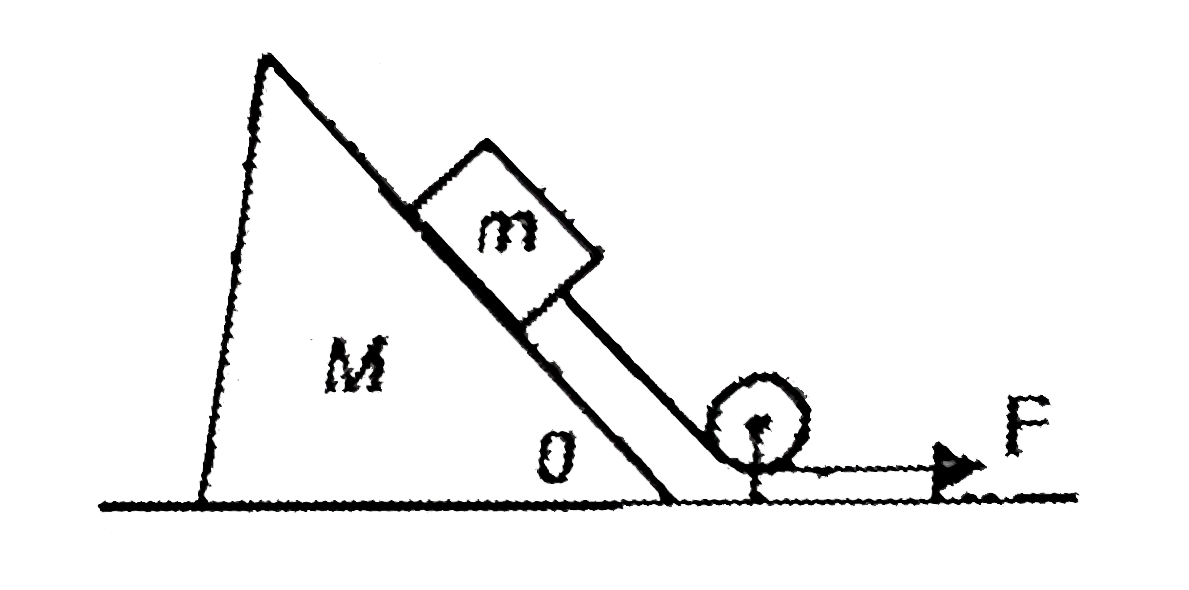
View SolutionIn the Fig. shown, mass 'm' is being pulled on the incline of a wedge of mass M. All the surface are smooth. Find the acceleration of the wedge.
View SolutionA plank of mass 3m is placed on a rough inclined plane and a man of mass m, the coefficient of friction between the board and inclined plane is μ=0.5, the minimum acceleration of man so that plank does not slide is :

View Solution

