For a quantum particle in a box, the lowest energy quantum state has 1/2 of the particle de Broglie wave fitting in the box. The next highest state corresponds to
1/4 de Broglie wavelength
1/2 de Broglie wavelength
1 de Broglie wavelength
2 de Broglie wavelength
The correct Answer is:C
Topper's Solved these Questions
- HYDROGEN ATOMBOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
15 Videos
- HYDROGEN ATOMBOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS (Linked Comprehension)
9 Videos
- HYDROGEN ATOMBOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PROBLEMS
36 Videos
- HEAT-MEASUREMENT AND TRANSFERBOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PRACTICE QUESTIONS( INTEGER TYPE)
5 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (Integer Type)
6 Videos
Similar Questions
A particle of mass m is trapped between two perfectly rigid parallel walls. The particle bounces back and forth between the walls without losing any energy. From a wave point of view, the particle trapped between the walls is like a standing wave in a stretched string between the walls. Distance between the two walls is L.
(a) Calculate the energy difference between third energy state and the ground state (lowest energy state) of the particle.
(b) Calculate the ground state energy if the mass of the particle is m=1mg and separation between the walls is L=1cm.
View SolutionChoose the correct alternatives
A. Ratio of de-Broglie wavelengths of proton and α-particle of same kinetic energy is 2L1
B. if neutron, α-particle and β-particle all are moving with same kinetic energy , β-particle has maximum de-Broglie wavelength
C. de-Broglie hypothesis treats particles as waves
D. de-Broglie hypothesis treats waves as made of particles
View Solution
Knowledge Check
Which of these particles having the same kinetic energy has the largest de Broglie wavelength ?
AElectronBAlpha particleCProtonDNeutronWhich of these particles having the same kinetic energy has the largest de Broglie wavelength ?
AElectronBAlpha particleCProtonDNeutronWhich of these particles (having the same kinetic energy) has the shortest de-Broglie wavelength ?
AElectronBAlpha-particleCProtonDNeutron
De-Broglie hypothesized that material particles have wave like properties. Figure shows a small particle in a box. The particle simply bounces back and forth at constant speed. As particles also have wave like properties it can be considered to be a wave reflecting back and forth from the ends of the box. The reflections will create a standing wave analogous to standing wave on a string tied at both ends. Since a standing wave confined to a region can have only selected wavelength, momentum of the particle is quantized. We can safely assume that such a particle only has kinetic energy. This energy must also be quantized.
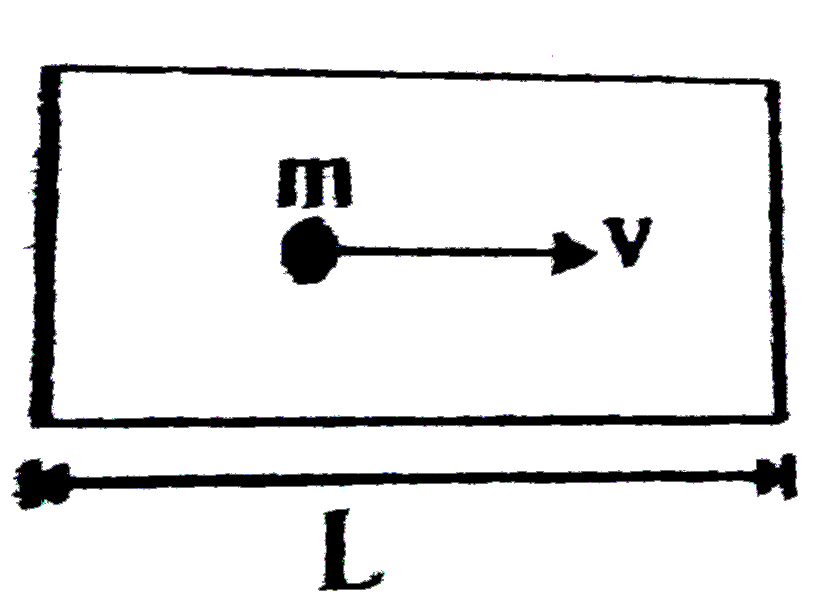
What is the particle's energy in n^(th) state?
View SolutionDe-Broglie hypothesized that material particles have wave like properties. Figure shows a small particle in a box. The particle simply bounces back and forth at constant speed. As particles also have wave like properties it can be considered to be a wave reflecting back and forth from the ends of the box. The reflections will create a standing wave analogous to standing wave on a string tied at both ends. Since a standing wave confined to a region can have only selected wavelength, momentum of the particle is quantized. We can safely assume that such a particle only has kinetic energy. This energy must also be quantized.
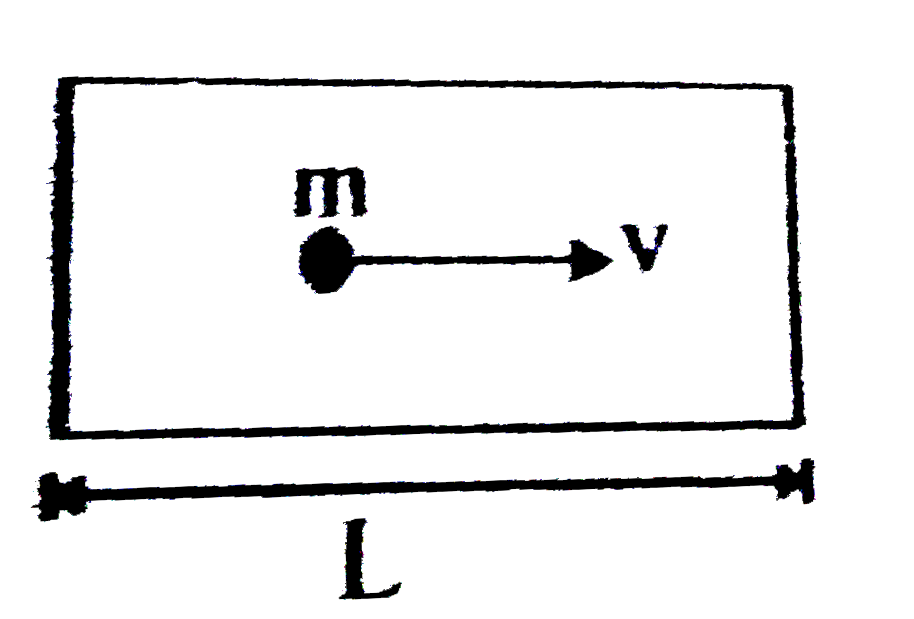
What is momentum of particle in n^(th) mode of standing wave ?
View SolutionDe-Broglie hypothesized that material particles have wave like properties. Figure shows a small particle in a box. The particle simply bounces back and forth at constant speed. As particles also have wave like properties it can be considered to be a wave reflecting back and forth from the ends of the box. The reflections will create a standing wave analogous to standing wave on a string tied at both ends. Since a standing wave confined to a region can have only selected wavelength, momentum of the particle is quantized. We can safely assume that such a particle only has kinetic energy. This energy must also be quantized.
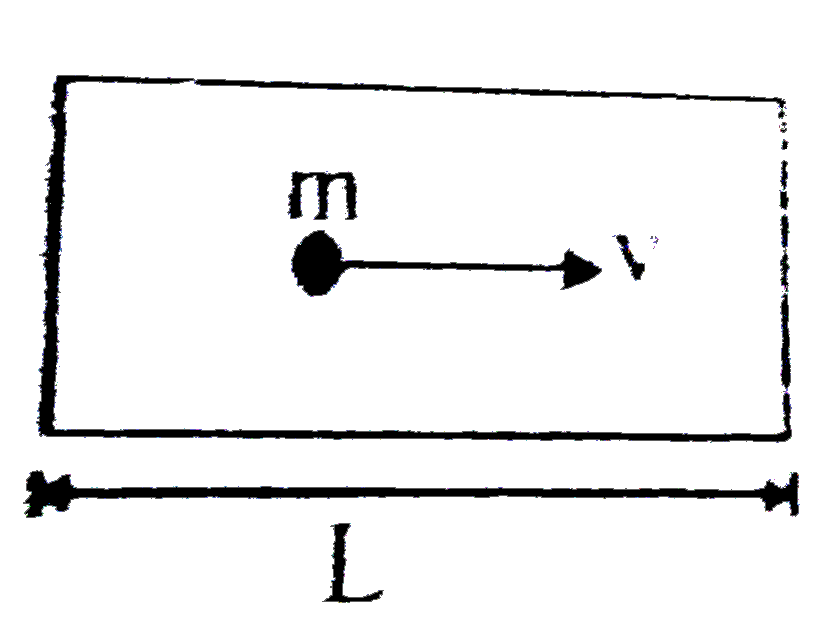
Mark the incorrect option.
View SolutionA particle of mass 'm' is projected from ground with velocity u making angle θ with the vertical. The de-Broglie wave length of the particle at the highest point is:
View SolutionWhich of the following particles - neutron, proton, electron and deuteron has the lowest energy if all have the same de Broglie wavelength
View Solution
