A beam of 35.0 keV electrons strikes a molybdenum target, generating the x rays whose spectrum is shown in Fig. What is the cutoff wavelength?
The correct Answer is:7
To find the cutoff wavelength for a beam of 35.0 keV electrons striking a molybdenum target, we can follow these steps:
Step 1: Understand the Concept of Cutoff Wavelength
The cutoff wavelength (λ_min) is the minimum wavelength of X-ray photons produced when electrons transfer all their energy to a single photon. This corresponds to the maximum energy of the photon generated.
Step 2: Use the Energy-Wavelength Relationship
The energy of a photon is related to its wavelength by the equation:
E=hcλ
Where:
- E is the energy of the photon,
- h is Planck's constant (6.626×10−34J s),
- c is the speed of light (3.0×108m/s),
- λ is the wavelength.
Step 3: Convert the Energy from keV to Joules
The energy of the electrons is given as 35.0 keV. We need to convert this to Joules.
1 eV = 1.6×10−19J, so:
35.0keV=35.0×103eV=35.0×103×1.6×10−19J
Calculating this gives:
E=5.6×10−15J
Step 4: Rearrange the Energy-Wavelength Equation
To find the cutoff wavelength, rearrange the equation:
λ=hcE
Step 5: Substitute the Values
Now substitute the values of h, c, and E:
λ=(6.626×10−34J s)(3.0×108m/s)5.6×10−15J
Step 6: Calculate the Wavelength
Perform the calculation:
λ=1.9878×10−25J m5.6×10−15J
λ≈3.55×10−11m
Step 7: Convert to Picometers
Since 1pm=10−12m:
λ≈35.5pm
Final Answer
The cutoff wavelength is approximately 35.5pm.
---
The cutoff wavelength (λ_min) is the minimum wavelength of X-ray photons produced when electrons transfer all their energy to a single photon. This corresponds to the maximum energy of the photon generated.
The energy of a photon is related to its wavelength by the equation:
E=hcλ
Where:
- E is the energy of the photon,
- h is Planck's constant (6.626×10−34J s),
- c is the speed of light (3.0×108m/s),
- λ is the wavelength.
The energy of the electrons is given as 35.0 keV. We need to convert this to Joules.
1 eV = 1.6×10−19J, so:
35.0keV=35.0×103eV=35.0×103×1.6×10−19J
Calculating this gives:
E=5.6×10−15J
To find the cutoff wavelength, rearrange the equation:
λ=hcE
Now substitute the values of h, c, and E:
λ=(6.626×10−34J s)(3.0×108m/s)5.6×10−15J
Perform the calculation:
λ=1.9878×10−25J m5.6×10−15J
λ≈3.55×10−11m
Since 1pm=10−12m:
λ≈35.5pm
The cutoff wavelength is approximately 35.5pm.
Topper's Solved these Questions
- ALL ABOUT ATOMS BOOK - RESNICK AND HALLIDAYCHAPTER - ALL ABOUT ATOMS EXERCISE - PROBLEMS
48 Videos
- ALL ABOUT ATOMS BOOK - RESNICK AND HALLIDAYCHAPTER - ALL ABOUT ATOMS EXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
57 Videos
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)
3 Videos
Similar Questions
The x rays shown are produced when 35.0 ke V electrons strike a molybdenum (Z=42) target. If the accelerating potential is maintained at this value but a silver (Z=47) target is used instead, what values of (a) λmin, (b) the wavelength of the Kα line, and (c ) the wavelength of the Kβ line result? The K, L, and M atomic x-ray levels for silver are 25.51, 3.56, and 0.53 keV.
View SolutionWhen electrons bombard a molybdenum target, they produce both continuous and characteristic x rays as shown in fig. In that figure the kinetic energy of the incident electrons is 35.0 keV, (a) what is the value of λmin, and (b) do the wavelengths of the KαandKβ lines increase, decrease, or remain the same?
View Solution
Knowledge Check
A beam of 35.0keV electrons strikes a molybdenum target, generating the X-rays. What is the cutoff wavelength ?
A35.5±B40.0±C15.95±D18.2±A beam of 350 keV electrons a molybdenum target, generating the X-rays. What is the cut-off wavelength?
A3.55 pmB400 pmC1595 pmD182 pm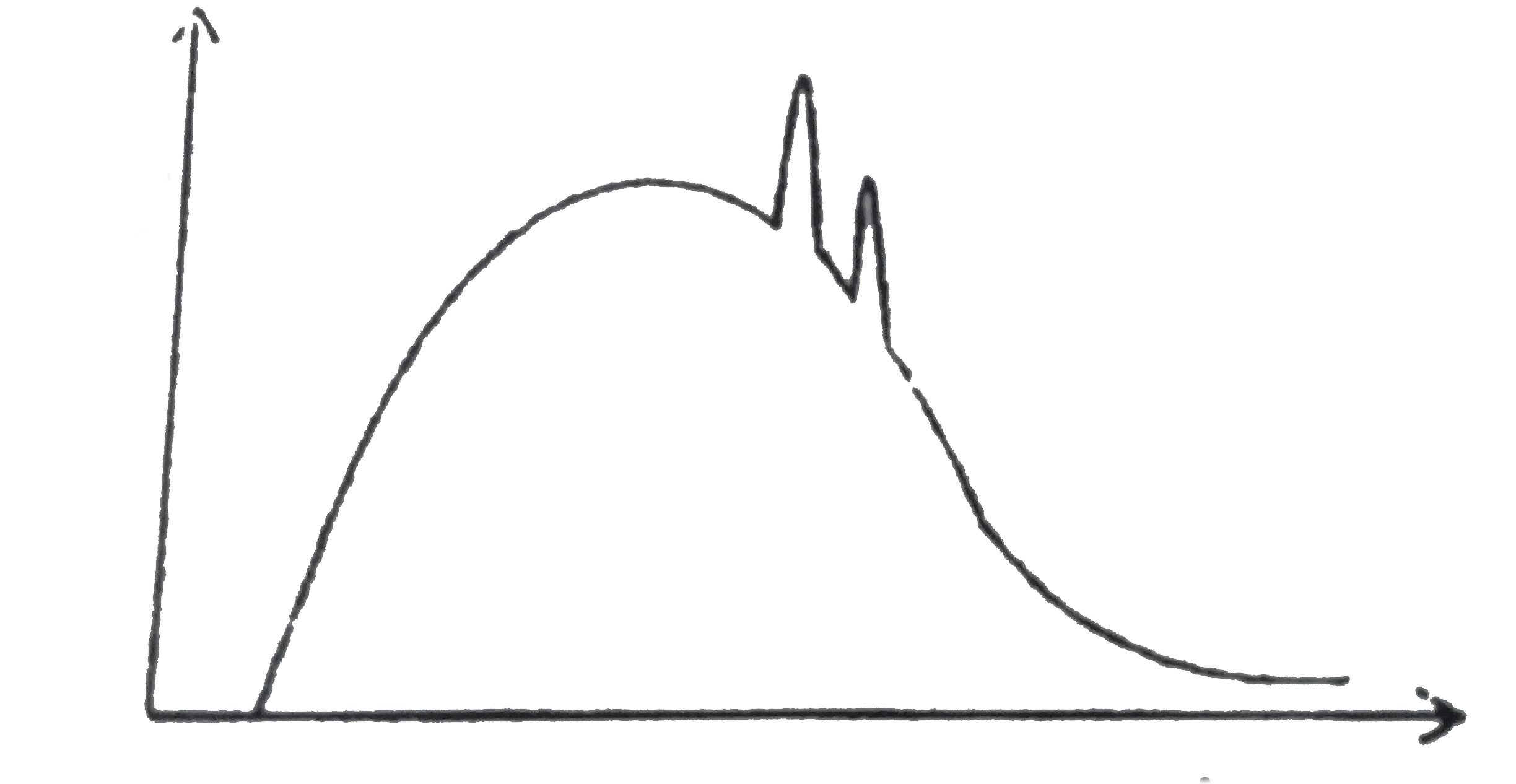
A beam of electrons striking a copper target produces X-rays. Its spectrum is as shown. Keeping the voltage same if the copper target is replaced with a different metal, the cut-off wavelength and characteristic lines of the new spectrum will change in comparison with old as:ACut-off wavelength will remain unchanged while characteristic lines will be different.Bboth cut-off wavelength and characteristic lines will remains unchangedCboth cut-off wavelength and characteristic lines will be different.Dcut-off wavelength wll be different while characteristic lines will remain unchanged.
A potential difference of 40,000 V is applied between the filament and the target metal inside X-ray tube. It is found that a current of 1 mA flows in the tube.
(i)How many electrons are hitting the target metal per second ?
(ii)Calculate the amount of energy falling on target metal per second in the form of kinetic energy of the electron .
(iii)What will be the cutoff wavelength of X-rays produced from this tube ?
View SolutionThe K-absorption edge of an unknown element is 0.171Å
a. Identify the element.
b. Find the average wavelength of the Kα,Kα,Kβ,Kγ lines.
c.
If a 100eV electron strikes the target of this element , what is the minimum wavelength of the x-ray emitted?
View SolutionWhen a beam of accelerated electrons hits a target , a continuous X - ray spectrum is emitted from the target. Which of the following wavelength is absent in X - ray spectrum , if the X - ray tube is operating at 40,000volts?
View SolutionA beam of electrons having energy 28 keV each strikes a target generating X rays. The minimum wave length λmin (called cut off wavelength ) of the X rays generated is
View SolutionThe characteristic of the electrons striking the target in an X-ray tube that, determines the intensity of X-rays is
View Solution
