In the helium-neon laser of laser action occurs between two excited states of the neon atom. However, in many lasers, laser action (lasing) occurs between the ground state and an excited state, as suggested in fig.
(a) Consider such a laser that emits at wavelength λ=550nm. If a population inversion is not generated what is the ratio of the population of atoms in state Ex to the population in the ground state E0, with the atoms at room temperature?
Text Solution
The naturally occurring population ratio Nx/N0 of the two states is due to thermal agitation of the gas atoms
Nx/N0=e−(Ex−E0)/kT (39-22)
To find Nx/N0 with we need to find the energy separation Ex−E0 between the two states. (2) We can obtain Ex−E0 from the given wavelength of 550 nm for the lasing between those two states.
The lasing wavelength gives us
Ex−E0=hf=hcλ
=(6.63×10−34J.s)(3.00×108m/s)(550×10−9m)(1.60×10−19J/eV)
=2.26eV.
We also need the mean energy of thermal agitation kT for an atom at room temperature (assumed to be 300 K), which is
kT=(8.62×10−5eV/K)(300K)=0.0259eV,
in which k is Boltzmann.s constant.
Substituting the last two results into give us the population ratio at room temperature:
Nx/N0=e−(2.26eV)(0.0259eV)
≈1.3×10−38
This is an extremely small number. It is not unreasonable, however. Atoms with a mean thermal agitation energy of only 0.0259 eV will not often impart an energy of 2.26 eV to another atom in a collision.
(b) For the conditions of (a), what temperature would the ratio Nx/N0 be 1/2?
Calculation: Now we want the temperature T such that thermal agiation has bumped enough neon atoms up to the higher-energy state to give Nx/N0=1/2. Substituting that ratio into taking the natural logarithm of both sides, and solving for T yield
T=Ex−E0k(ln2)=2.26eV(8.62×10−5eV/K)(ln2)
=38000K.
This is much hotter than the surface of the Sun. Thus, it is clear that if we are to invert the population of these two levels, some specific mechanism for bringing this about is needed-that is, we must ..pump.. the atoms. No temperature, however high, will naturally generate a population inversion by thermal agitation.
|
Topper's Solved these Questions
- ALL ABOUT ATOMS BOOK - RESNICK AND HALLIDAYCHAPTER - ALL ABOUT ATOMS EXERCISE - PROBLEMS
48 Videos
- ALL ABOUT ATOMS BOOK - RESNICK AND HALLIDAYCHAPTER - ALL ABOUT ATOMS EXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
57 Videos
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)
3 Videos
Similar Questions
Knowledge Check
What is the ratio of the population of state A in 2003 to the population of stateE in 2007?
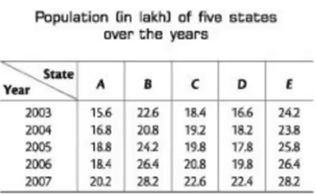 A37:22B22:37C47:26D26:47
A37:22B22:37C47:26D26:47Laser is/ are
AHighly coherentBHighly monochromaticCHighly directionalDAll of these
Lasers are used in
View SolutionWhat is the basis of laser action?
View SolutionWhat is a laser ?
View SolutionLaser is the acronym for
View SolutionAn excited state of H atom emits a photon of wavelength λ and returns in the ground state. The principal quantum number of excited state is given by:
View SolutionAn excited state of H atom emits a photon of wavelength λ and returns in the ground state. The principal quantum number of excited state is given by:
View Solution
