Column IColumn II(A)For a stationary wave(p)Vibrations are perpendicular to direction to wave propagation(B)For a longitudinal wave(q)Amplitude of vibrations changes with time(C)For a transverse wave(r)Amplitude of vibration does not change with time(D)For a progressive wave(s)Vibrations are along the direction of wave propagation(t)Nodes and antinoes are formed
The correct Answer is:A→(r,t) B→(q,s) C→(p,q) D→(p,q,s)
To solve the problem of matching the items in Column I with those in Column II, we need to analyze each statement in Column I and determine which statements in Column II are applicable to them.
1. For a stationary wave (A):
- Vibrations are perpendicular to direction of wave propagation (p): This is incorrect. In a stationary wave, the wave does not propagate, so there is no direction of propagation.
- Amplitude of vibrations changes with time (q): This is incorrect. In a stationary wave, the amplitude is fixed at each point and does not change with time.
- Amplitude of vibration does not change with time (r): This is correct. The amplitude remains constant at each point in a stationary wave.
- Vibrations are along the direction of wave propagation (s): This is incorrect. Again, since the wave is stationary, there is no direction of propagation.
- Nodes and antinodes are formed (t): This is correct. Stationary waves have fixed points (nodes) where there is no displacement and points of maximum displacement (antinodes).
Matching for A: R, T
2. For a longitudinal wave (B):
- Vibrations are perpendicular to direction of wave propagation (p): This is incorrect. In a longitudinal wave, the vibrations are parallel to the direction of wave propagation.
- Amplitude of vibrations changes with time (q): This is correct. In a longitudinal wave, as the wave travels, the amplitude can change due to energy loss.
- Amplitude of vibration does not change with time (r): This is incorrect. As mentioned, the amplitude can change over time.
- Vibrations are along the direction of wave propagation (s): This is correct. In a longitudinal wave, the particles move back and forth in the same direction as the wave travels.
- Nodes and antinodes are formed (t): This is incorrect. Longitudinal waves do not form nodes and antinodes in the same way as stationary waves.
Matching for B: Q, S
3. For a transverse wave (C):
- Vibrations are perpendicular to direction of wave propagation (p): This is correct. In a transverse wave, the vibrations are indeed perpendicular to the direction of wave propagation.
- Amplitude of vibrations changes with time (q): This can be correct depending on the context, but generally, in a simple transverse wave, the amplitude remains constant unless specified otherwise.
- Amplitude of vibration does not change with time (r): This is also generally correct for ideal transverse waves.
- Vibrations are along the direction of wave propagation (s): This is incorrect. In a transverse wave, the vibrations are perpendicular, not along the direction of propagation.
- Nodes and antinodes are formed (t): This is correct. Transverse waves can also form nodes and antinodes.
Matching for C: P, R, T
4. For a progressive wave (D):
- Vibrations are perpendicular to direction of wave propagation (p): This can be correct if the progressive wave is transverse.
- Amplitude of vibrations changes with time (q): This is correct. In a progressive wave, the amplitude can change as the wave travels.
- Amplitude of vibration does not change with time (r): This is incorrect. Progressive waves can have changing amplitudes.
- Vibrations are along the direction of wave propagation (s): This is correct. In a longitudinal progressive wave, the vibrations are along the direction of propagation.
- Nodes and antinodes are formed (t): This is incorrect. Progressive waves do not form nodes and antinodes like stationary waves.
Matching for D: Q, S, P (if considering transverse)
Final Matches:
- A: R, T
- B: Q, S
- C: P, T
- D: Q, S (and P if considering transverse)
- Vibrations are perpendicular to direction of wave propagation (p): This is incorrect. In a stationary wave, the wave does not propagate, so there is no direction of propagation.
- Amplitude of vibrations changes with time (q): This is incorrect. In a stationary wave, the amplitude is fixed at each point and does not change with time.
- Amplitude of vibration does not change with time (r): This is correct. The amplitude remains constant at each point in a stationary wave.
- Vibrations are along the direction of wave propagation (s): This is incorrect. Again, since the wave is stationary, there is no direction of propagation.
- Nodes and antinodes are formed (t): This is correct. Stationary waves have fixed points (nodes) where there is no displacement and points of maximum displacement (antinodes).
- Vibrations are perpendicular to direction of wave propagation (p): This is incorrect. In a longitudinal wave, the vibrations are parallel to the direction of wave propagation.
- Amplitude of vibrations changes with time (q): This is correct. In a longitudinal wave, as the wave travels, the amplitude can change due to energy loss.
- Amplitude of vibration does not change with time (r): This is incorrect. As mentioned, the amplitude can change over time.
- Vibrations are along the direction of wave propagation (s): This is correct. In a longitudinal wave, the particles move back and forth in the same direction as the wave travels.
- Nodes and antinodes are formed (t): This is incorrect. Longitudinal waves do not form nodes and antinodes in the same way as stationary waves.
- Vibrations are perpendicular to direction of wave propagation (p): This is correct. In a transverse wave, the vibrations are indeed perpendicular to the direction of wave propagation.
- Amplitude of vibrations changes with time (q): This can be correct depending on the context, but generally, in a simple transverse wave, the amplitude remains constant unless specified otherwise.
- Amplitude of vibration does not change with time (r): This is also generally correct for ideal transverse waves.
- Vibrations are along the direction of wave propagation (s): This is incorrect. In a transverse wave, the vibrations are perpendicular, not along the direction of propagation.
- Nodes and antinodes are formed (t): This is correct. Transverse waves can also form nodes and antinodes.
- Vibrations are perpendicular to direction of wave propagation (p): This can be correct if the progressive wave is transverse.
- Amplitude of vibrations changes with time (q): This is correct. In a progressive wave, the amplitude can change as the wave travels.
- Amplitude of vibration does not change with time (r): This is incorrect. Progressive waves can have changing amplitudes.
- Vibrations are along the direction of wave propagation (s): This is correct. In a longitudinal progressive wave, the vibrations are along the direction of propagation.
- Nodes and antinodes are formed (t): This is incorrect. Progressive waves do not form nodes and antinodes like stationary waves.
- A: R, T
- B: Q, S
- C: P, T
- D: Q, S (and P if considering transverse)
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - INTEGER TYPE QUESTION13videos
WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - MATCHING TYPE QUESTIONS3videos
WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - UNITS AND MEASUREMENTEXERCISE - CHAPTER PRACTICE TEST15videos
UNITS AND MEASUREMENT
- BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Chapter Practice Test16videos
WORK, ENERGY AND POWER
Similar Questions
State the general name of the waves in which the particles of the medium vibrate:
(i) in the same direction as wave.
(ii) at right angles to the direction of wave.View SolutionIn a __________________ wave particles of the medium vibrate in a direction parallel to the direction of wave propagation.
View Solution
Knowledge Check
- Question 1 - Select One
Amplitude of vibration in stationary wave is
Amaximum at nodes.Bzero at nodesCmaximum at nodes and antinodesDequal to all the points - Question 2 - Select One
In a stationary waves, the amplitude of vibrating paticles
ARemains constantBZeroCVaries from particle to particleDMaximum - Question 3 - Select One
In a ________wave particles of the medium vibrate in a direction perpendicular to the direction of wave propagation.
AlongitudinalBrollingCtransverseDfield
If the direction of the vibration of particles is parallel to the direction of the propagation of a wave , then the wave is
View Solution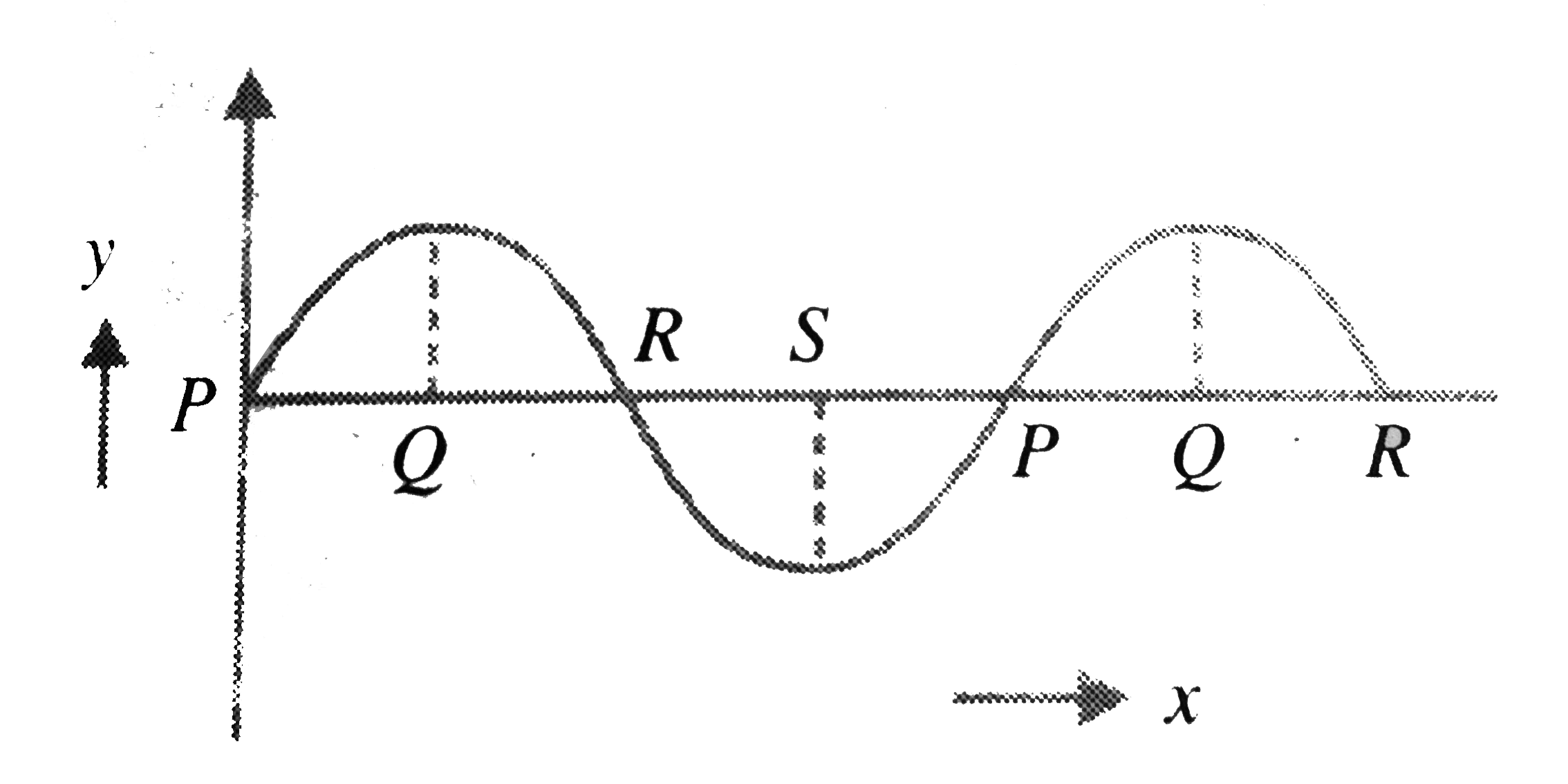
Figure. Represents the displacement y versus distance x along the direction of propagation of a longitudinal wave. The pressure is maximum at position markedView SolutionThe waves in which the particles of the medium vibrate in a direction perpendicular to the direction of wave motion is known as
View SolutionIn the propagation of polarised light waves, the angle between the plane of vibration and the plane of polarization is
View SolutionStatement I:In a progressive logitudinal wave, the amplitude of the wave will not be the same at all points of the medium along the direction of motion of the wave.
Statement II: there is a continuous change of the phase angle of the wave as it progressive in the direction of motion.View Solution

