A student obtains resistances 3, 4, 12 and 16 Ohm using only two metallic resistors either separately or joined together. What is the resistance of each of the resistors?
To solve the problem of finding the resistance values of two resistors (R1 and R2) that can produce the equivalent resistances of 3, 4, 12, and 16 Ohms using series and parallel combinations, we can follow these steps:
Step 1: Identify the possible combinations
We know that we can connect two resistors in series or in parallel. The formulas for the equivalent resistance in these configurations are:
- Series: Rseries=R1+R2
- Parallel: Rparallel=R1⋅R2R1+R2
Step 2: List the given resistances
The resistances we need to achieve are: 3 Ohms, 4 Ohms, 12 Ohms, and 16 Ohms.
Step 3: Analyze the maximum resistance
The maximum resistance (16 Ohms) must be the sum of the two resistors in series. Therefore, we can set up the equation:
R1+R2=16
Step 4: Analyze the minimum resistance
The minimum resistance (3 Ohms) must be the result of the two resistors in parallel. Therefore, we can set up the equation:
R1⋅R2R1+R2=3
Step 5: Substitute R2 in terms of R1
From the first equation R1+R2=16, we can express R2 as:
R2=16−R1
Step 6: Substitute R2 in the parallel resistance equation
Substituting R2 into the parallel resistance equation gives:
R1⋅(16−R1)R1+(16−R1)=3
This simplifies to:
R1⋅(16−R1)16=3
Step 7: Solve the equation
Multiplying both sides by 16:
R1⋅(16−R1)=48
Expanding this gives:
16R1−R12=48
Rearranging leads to:
R12−16R1+48=0
Step 8: Factor or use the quadratic formula
We can factor this quadratic equation:
(R1−12)(R1−4)=0
Thus, R1=12 or R1=4.
Step 9: Find corresponding R2
If R1=12, then:
R2=16−12=4
If R1=4, then:
R2=16−4=12
Conclusion
The resistances of the two resistors are:
- R1=12 Ohms
- R2=4 Ohms
We know that we can connect two resistors in series or in parallel. The formulas for the equivalent resistance in these configurations are:
- Series: Rseries=R1+R2
- Parallel: Rparallel=R1⋅R2R1+R2
The resistances we need to achieve are: 3 Ohms, 4 Ohms, 12 Ohms, and 16 Ohms.
The maximum resistance (16 Ohms) must be the sum of the two resistors in series. Therefore, we can set up the equation:
R1+R2=16
The minimum resistance (3 Ohms) must be the result of the two resistors in parallel. Therefore, we can set up the equation:
R1⋅R2R1+R2=3
From the first equation R1+R2=16, we can express R2 as:
R2=16−R1
Substituting R2 into the parallel resistance equation gives:
R1⋅(16−R1)R1+(16−R1)=3
This simplifies to:
R1⋅(16−R1)16=3
Multiplying both sides by 16:
R1⋅(16−R1)=48
Expanding this gives:
16R1−R12=48
Rearranging leads to:
R12−16R1+48=0
We can factor this quadratic equation:
(R1−12)(R1−4)=0
Thus, R1=12 or R1=4.
If R1=12, then:
R2=16−12=4
If R1=4, then:
R2=16−4=12
The resistances of the two resistors are:
- R1=12 Ohms
- R2=4 Ohms
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (ADDITIONAL QUESTIONS)11videos
CURRENT ELECTRICITY
- BOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (FILL IN THE BLANKS)10videos
CURRENT ELECTRICITY
- BOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - HIGHER ORDER THINKING SKILLS & ADVANCED LEVEL10videos
CURRENT ELECTRICITY
- BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test16videos
ATOMS
- BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST15videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
The effective resistance of two resistors in parallel is 127Ω. If one of the resistors is disconnected the resistance becomes 4Ω. The resistance of the other resistor is
A4ΩB3ΩC127ΩD712Ω - Question 2 - Select One
A technician has only two resistance coils. By using them in series or in parallel he is able to obtain the resistance 3,4,12 and 16 ohm. The resistance of two coils are
A6 and 10 ohmsB4 and 12 ohmsC7 and 9 ohmsD4 and 16 ohms - Question 3 - Select One
If all resistors in the shown network are of equal resistance, and the battery is of emf equal to 10 V and internal resistance equal to 1Ω, what should be resistance of each resistor so that the battery delivers maximum power
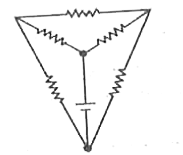 A1ΩB2OmeggaC3ΩD4Ω
A1ΩB2OmeggaC3ΩD4Ω
A circuit consisting of five resistors each of resistance R, forming a wheatstone bridge. What is the equivalent resistance of the circuit?
View SolutionWhat is the minimum resistance that can be obtained using four resistors of 5 Ohm each?
View SolutionThree resistors each of 2 ohm are connected together in a triangular shape. The resistance between any two vertices will be
View SolutionA technician has only two resistance coils. By using them in series or in parallel he is able to obtain the resistance 3,4,12 and 16 ohm. The resistance of two coils are
View SolutionTwo resistors are connected (a) in series (b) in parallel. The equivalent resistance in the two cases are 9 ohm and respectively. Then the resistances of the component resistors are
View Solution


