With the help of circuit diagram, explain how a meter bridge can be used to find unknown resistance of a given wire?
To find the unknown resistance of a wire using a meter bridge, we can follow these steps:
1. Understanding the Meter Bridge Setup:
- A meter bridge is based on the principle of the Wheatstone bridge. It consists of a one-meter long wire of uniform resistance, which is connected in a circuit with a galvanometer and a jockey.
2. Circuit Diagram:
- Draw a circuit diagram of the meter bridge. The diagram should include:
- A straight wire of length 1 meter (the bridge wire).
- Two known resistances (R1 and R2) connected in the two gaps of the bridge.
- A galvanometer (G) connected across the bridge wire.
- A jockey (J) used to touch the wire at different points.
R1GR2⊢−−−−−−−−⊢−−−−−−−||||∣|||||⊢−−−−−−−−⊢−−−−−−−|∣|∣|J(Jockey)
3. Connecting the Circuit:
- Connect the known resistance \( R1 \) in one arm of the bridge and the unknown resistance \( X \) in the other arm. The galvanometer is connected between the two points of the bridge wire.
4. Finding the Null Point:
- Move the jockey along the wire until you find a point where the galvanometer shows zero deflection. This point is known as the null point.
5. Measuring Lengths:
- Let the distance from one end of the meter bridge to the jockey be \( l \) (in cm), and the remaining length of the wire will be \( 100 - l \) (since the total length of the wire is 100 cm).
6. Applying the Wheatstone Bridge Principle:
- At the null point, the ratio of the resistances is given by:
\(
\frac{R1}{X} = \frac{l}{100 - l}
\)
- Rearranging gives:
\(
X = R1 \cdot \frac{100 - l}{l}
\)
7. Calculating Unknown Resistance:
- Substitute the known values of \( R1 \) and the measured length \( l \) into the equation to calculate the unknown resistance \( X \).
- A meter bridge is based on the principle of the Wheatstone bridge. It consists of a one-meter long wire of uniform resistance, which is connected in a circuit with a galvanometer and a jockey.
- Draw a circuit diagram of the meter bridge. The diagram should include:
- A straight wire of length 1 meter (the bridge wire).
- Two known resistances (R1 and R2) connected in the two gaps of the bridge.
- A galvanometer (G) connected across the bridge wire.
- A jockey (J) used to touch the wire at different points.
- Connect the known resistance \( R1 \) in one arm of the bridge and the unknown resistance \( X \) in the other arm. The galvanometer is connected between the two points of the bridge wire.
- Move the jockey along the wire until you find a point where the galvanometer shows zero deflection. This point is known as the null point.
- Let the distance from one end of the meter bridge to the jockey be \( l \) (in cm), and the remaining length of the wire will be \( 100 - l \) (since the total length of the wire is 100 cm).
- At the null point, the ratio of the resistances is given by:
\(
\frac{R1}{X} = \frac{l}{100 - l}
\)
- Rearranging gives:
\(
X = R1 \cdot \frac{100 - l}{l}
\)
- Substitute the known values of \( R1 \) and the measured length \( l \) into the equation to calculate the unknown resistance \( X \).
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:REVISION EXERCISES (LONG ANSWER QUESTIONS)
Explore 10 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:REVISION EXERCISES (NUMERICAL PROBLEMS)
Explore 24 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:REVISION EXERCISES (FILL IN THE BLANKS)
Explore 10 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
Explain the use of a metre bridge for finding unknown resistance.
View SolutionA meter bridge cannot be used to measure …… resistances
View SolutionDraw a circuit diagram of a meter bridge used to determine the unknown resistance R of a given wire. Hence derive the expression for R in terms of the known resistance S.
View SolutionWrite the principle of working of a potentiometer. Describe briefly, with the help of a circuit diagram, how a potentiometer is used to determine the internal resistance of a cell.
View SolutionWith the help of a circuit diagram, explain the working principle of a metre bridge. How is it used to determine the unknown resistance of a given wire? Write the necessary precautions to minimise the error in the result?
View SolutionWith the help of a circuit diagram, explain the working principle of metre bridge. How is it used to determine the unknown resistance of a given wire ? Write the necessary precautions to minimise error in the result.
View SolutionExplain sensitivity of moving coil galvanometer. Show with the help of a circuit diagram that how a moving coil galvanometer can be converted into an ammeter of given range. Write necessary mathematical relation. What is the resistance of ideal ammeter?
View SolutionWith the help of a labelled circuit diagram, explain how an n-p-n transistor can be used as an amplifier in common-emitter configuration. Explain how the input and output voltages are out of phase by 1800 for a common-emitter transistor amplifier.
View SolutionState the principle of potentiometer. With the help of circuit diagram, describe a method to find the internal resistance of a primary cell.
View Solution(a) With the help of a circuit diagram, obtain the relation for the equivalent resistance of two resistances connected in parallel.
(b) In the circuit diagram shown below, find:
(i) Total resistance.
(ii) Current shown by the ammeter A
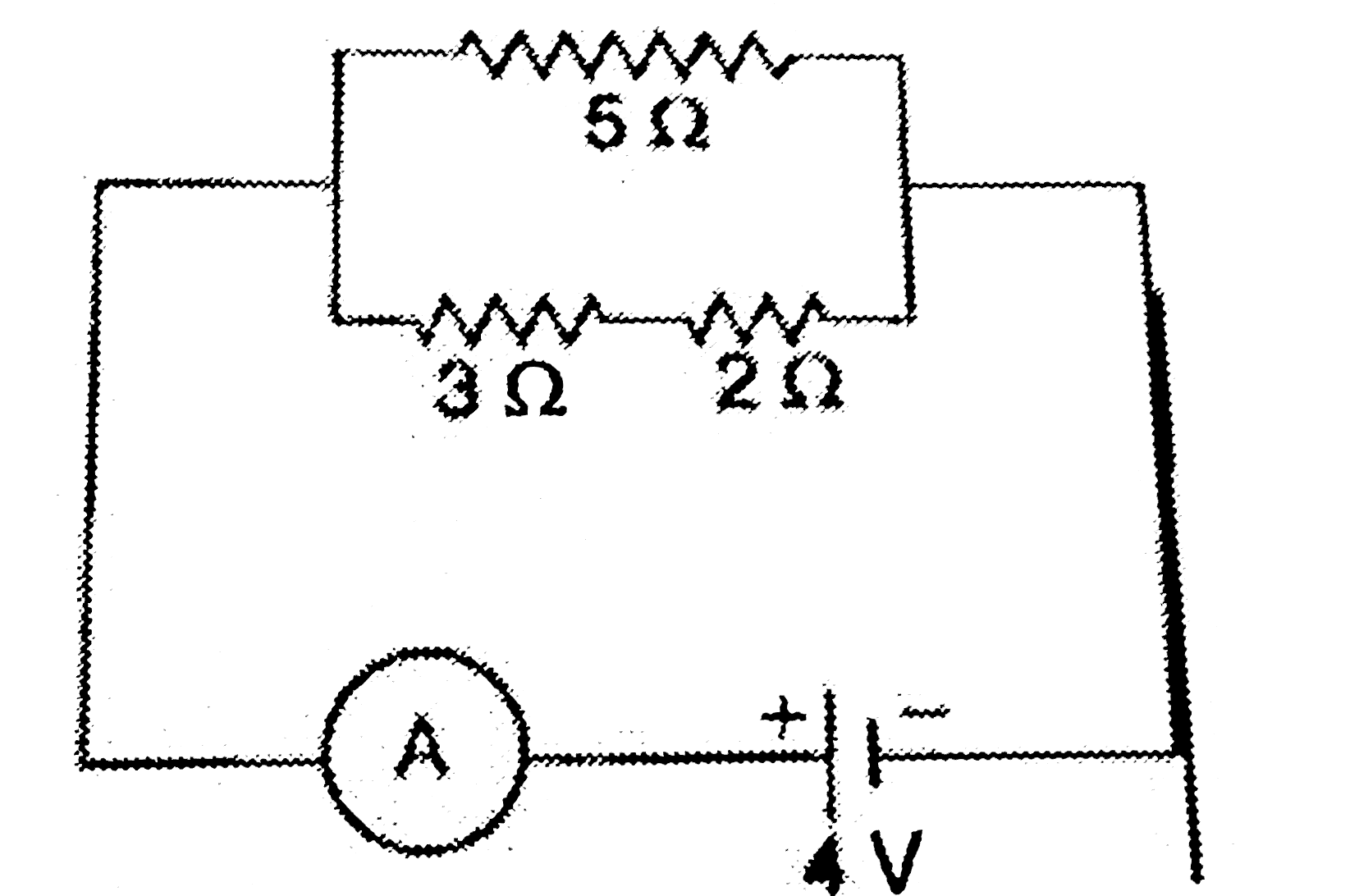
View Solution
