Assertion: Two identical cells of emf E and internal resistance r are connected to each other in such a manner that the positive terminal of one is connected to the positive terminal of the other. The net emf of its combination will be E.
Reason: Effective internal resistance of this combination will be r/2
If both assertion and reason are correct and reason is a correct explanation of the assertion
If both assertion and reason are correct but reason is not the correct explanation of the assertion
If assertion is correct but reason is incorrect
If assertion is incorrect but reason is correct
The correct Answer is:B
To solve the question, we need to analyze the assertion and reason provided regarding the combination of two identical cells.
1. Understanding the Configuration:
- We have two identical cells, each with an EMF (E) and internal resistance (r).
- The cells are connected in such a way that the positive terminal of one cell is connected to the positive terminal of the other cell. This configuration is essentially a parallel connection.
2. Net EMF Calculation:
- In a parallel connection of identical cells, the net EMF (E_net) remains the same as the EMF of one cell. Therefore, the net EMF of the combination is:
Enet=E
- This confirms that the assertion is true: "The net EMF of its combination will be E."
3. Effective Internal Resistance Calculation:
- The internal resistances of the two cells are also in parallel. The formula for the equivalent resistance (R_eq) of two resistors (r) in parallel is given by:
1Req=1r+1r=2r
- Therefore, the equivalent internal resistance is:
Req=r2
- This confirms that the effective internal resistance of the combination is R/2, which supports the reason provided.
4. Conclusion:
- Both the assertion and the reason are true:
- The assertion is true because the net EMF of the combination is E.
- The reason is true because the effective internal resistance of the combination is R/2.
- However, the reason does not explain the assertion directly, as the assertion is based on the nature of EMF in parallel connections, while the reason is based on the calculation of internal resistance.
Final Answer:
- The assertion is true, and the reason is true, but the reason does not explain the assertion. Therefore, the correct option is that both are true, but they do not explain each other.
- We have two identical cells, each with an EMF (E) and internal resistance (r).
- The cells are connected in such a way that the positive terminal of one cell is connected to the positive terminal of the other cell. This configuration is essentially a parallel connection.
- In a parallel connection of identical cells, the net EMF (E_net) remains the same as the EMF of one cell. Therefore, the net EMF of the combination is:
Enet=E
- This confirms that the assertion is true: "The net EMF of its combination will be E."
- The internal resistances of the two cells are also in parallel. The formula for the equivalent resistance (R_eq) of two resistors (r) in parallel is given by:
1Req=1r+1r=2r
- Therefore, the equivalent internal resistance is:
Req=r2
- This confirms that the effective internal resistance of the combination is R/2, which supports the reason provided.
- Both the assertion and the reason are true:
- The assertion is true because the net EMF of the combination is E.
- The reason is true because the effective internal resistance of the combination is R/2.
- However, the reason does not explain the assertion directly, as the assertion is based on the nature of EMF in parallel connections, while the reason is based on the calculation of internal resistance.
- The assertion is true, and the reason is true, but the reason does not explain the assertion. Therefore, the correct option is that both are true, but they do not explain each other.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (D. MULTIPLE CHOICE QUESTIONS MATRIX MATCH TYPE QUESTIONS)
1 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (D. MULTIPLE CHOICE QUESTIONS INTEGER TYPE QUESTIONS)
11 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (D. MULTIPLE CHOICE QUESTIONS BASED ON A GIVEN PASSAGE/COMPREHENSION)
15 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
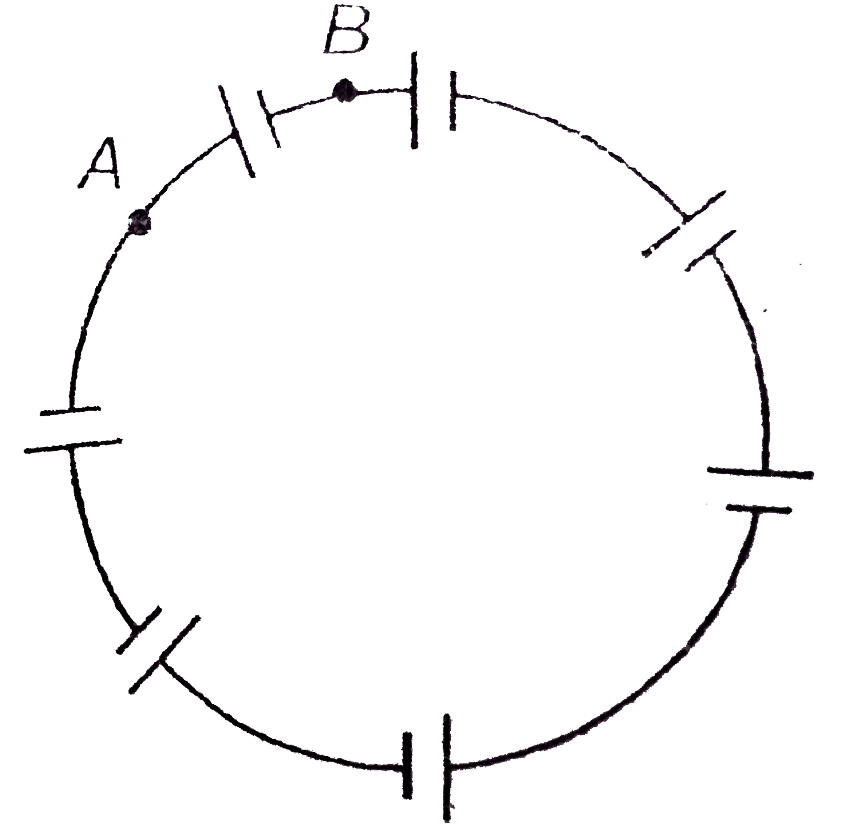
Seven identical cells each of e.m.f. E and internal resistance r are connected as shown . The potential difference between A and B is
View Solutionn-identical cells each of emf E and internal resistance r are connected in series. Find the expression for current in the circuit given below

View Solution
Knowledge Check
If n cells each of emf E and internal resistance are connected in parallel, then the total emf and internal resistances will be
Aε,rnBε,nrCnε,rnDnε,nrFour identical cells of emf ε and internal resistance r are to be connected in series. Suppose, if one of the cell is connected wrongly, then the equivalent emf and effective internal resistance of the combination is
A2E and 4rB4E and 4rC2E and 2rD4E and 2rn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
AnER+nrBnEnR+rCER+nrDnER+r
n' cells , each of emf 'e' and internal resistance 'r' are connected in a closed circuit so that the positive terminal of a cell is joined to the negative terminal of the next, as shown in figure. Any two points of the circuit are connected by an external resistance R. Find the current in R.
View SolutionA group of six identical cells each of emf E and internal resistance r are joined in series to from a loop. The terminal voltage across each cell is
View Solutionn' cells , each of emf 'e' and internal resistance 'r' are connected in a closed circuit so that the positive terminal of a cell is joined to the negative terminal of the next, as shown in figure. Any two points of the circuit are connected by an external resistance R. Find the current in R.
View SolutionFive cells each of e.m.f E and internal resistance r are connected in series. If due to over sight, one cell is connected wrongly ,the equivalent e.m.f of the combination is
View SolutionA cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
View Solution
