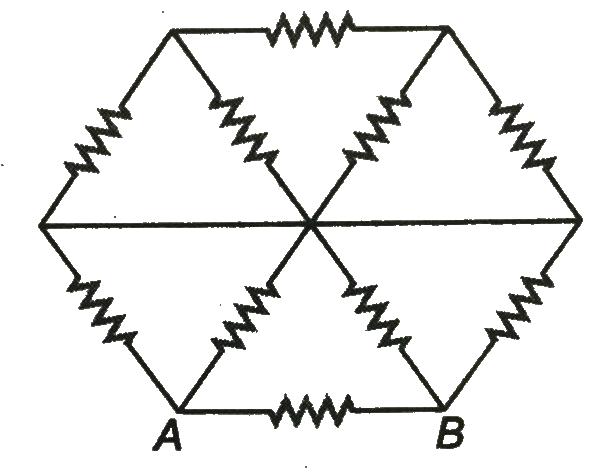
Each resistor in the network is of resistance . What will be the equivalent resistance between A and B?


Text Solution
The correct Answer is:3
In the upper part of the network we can use the concept of a balanced Wheatstone bridge and thus branch CD and EF will carry no electric current. We can remove the resistors along CD and EF. Thus, it is clear that three resistors of connected in series will have equivalent resistance of . Thus, resistances will be in parallel to give effective resistance of
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (NCERT EXEMPLAR PROBLEMS)
11 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Chapter Practice Test
15 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (D. MULTIPLE CHOICE QUESTIONS MATRIX MATCH TYPE QUESTIONS)
1 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Knowledge Check
In the network of resistors shown in the adjoining figure, the equivalent resistance between A and B is
 A54 ohmB18 ohmC36 ohmD9 ohm
A54 ohmB18 ohmC36 ohmD9 ohmEach resistance in the given network has the value of 10Ω.The equivalent resistance between, A and B will be: :
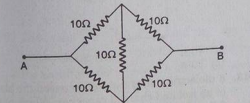 A30ΩB10ΩC20ΩD2Ω
A30ΩB10ΩC20ΩD2ΩEach resistance in the given network has the value of 10Ω.The equivalent resistance between, A and B will be: :
 A30ΩB10ΩC20ΩD2Ω
A30ΩB10ΩC20ΩD2Ω
In the adjoining network of resistors each is of resistance rΩ. Find the equivalent resistance between A and B.
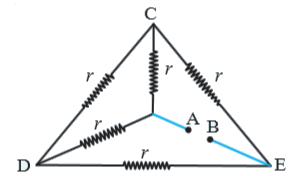
View SolutionIn the adjoining network of resistors each is of resistance rΩ. Find the equivalent resistance between A and B.

View SolutionIn the network of resistors shown in the adjoining figure, the equivalent resistance between A and B is

View SolutionShown in the figure is an infinite network of resistors each of resistance 1Ω . The effective resistance in between A and B is

View SolutionEach resistor shown in figure is an infinite network of resistance1Ω. The effective resistance Between points A and B is
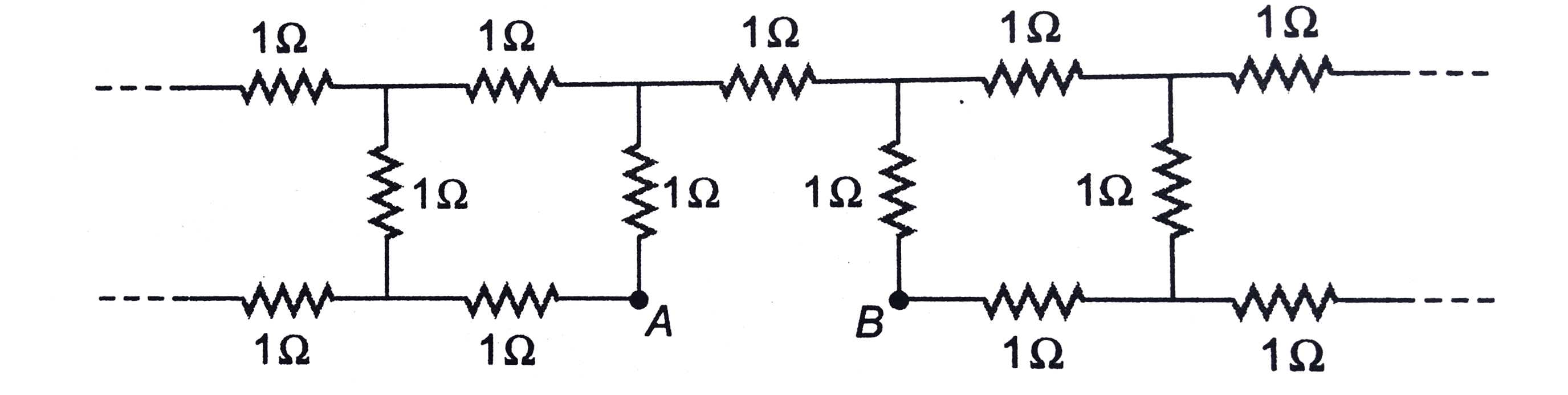
View Solution