Prove that for two half reactions having potentials E1 and E2 which are combined to yield a third half reaction, having a potential E3,
E3=n1E1+n2E2n3
Let ΔG1,ΔG2 and ΔG3 are the free energy changes for the half cell reactions having potentials E1,E2 and E3 respectively , then
ΔG3=ΔG1+ΔG2
Since ΔG=-nFE
or −n3FE3=−n1FE1−n2FE2
Dividing both sides by −n3F
E3=n1E1+n2E2n3
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROCHEMISTRY EXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS) (MULTIPLE CHOICE QUESTIONS )35videos
ELECTROCHEMISTRY
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROCHEMISTRY EXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS) B MULTIPLE CHOICE QUESTIONS77videos
ELECTROCHEMISTRY
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROCHEMISTRY EXERCISE - REVISION EXERCISES OBJECTIVE QUESTIONS Long Answer Questions11videos
ELECTROCHEMISTRY
- BOOK - MODERN PUBLICATIONCHAPTER - D AND F-BLOCK ELEMENTSEXERCISE - UNIT PRACTICE TEST12videos
D AND F-BLOCK ELEMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - GENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTSEXERCISE - COMPETION FILE (Integer Type Numerical Value Type Questions)5videos
GENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTS
Similar Questions
Statement : If two half reaction with electrode potential E∘1 and E∘2 gives a third reaction then,
ΔG∘3=ΔG∘1+ΔG∘2
Explanation : E∘3=E∘1+E∘2View SolutionThree coins are tossed. Let E1 denotes "Three heads or three tails" E2, denotes ''at least two heads'' and E3, denotes'' at most two tails''. Which of the following pairs (E1,E2),(E1,E3)and(E2,E3) arindependent and which are not ?
View Solution
Knowledge Check
- Question 1 - Select One
Statement : If two half reaction with electrode potential E∘1 and E∘2 gives a third reaction then,
ΔG∘3=ΔG∘1+ΔG∘2
Explanation : E∘3=E∘1+E∘2ASTATEMENT-1 is True, STATEMENT-2 is True, STATEMENT -2 is correct explanation for STATEMENT-1BSTATEMENT 1 is True, STATEMENT-2 Is True, STATEMENT -2 is NOT a correct explanation for STATEMENT-1CSTATEMENT - 1 is True, STATEMENT-2 is FalseDSTATEMENT-1 is False, STATEMENT-2 is True - Question 2 - Select One
when two half-cells of electrode potential of E1 and E2 are combined to form a half cell of electrode potential E3 , then
(when n1,n2andn3 are no. of electrons exchanged in first second and combined half-cells:AE3=E2−E1BE3=E1n1+E2n2n3CE3=E1n1+E2n2n23DE3=E1−E2 - Question 3 - Select One
Read the following passage for the evaluation of E∘ when different number of electrons are involved. Consider addition of the following half reactions
(1) Fe3+(aq)+3e−→Fe(s)E∘1=0.45V
(2) Fe(s)→Fe2+(aq)+2e−E∘2=−0.04V
(3) Fe3+(aq)+e−→Fe2+(aq)E∘3=?
Because half-reactions (1) and (2) contains a different number of electrons, the net reaction (3) is another half-reaction and E∘3 can't be obtained simply by adding E∘1 and E∘3. The free - energy changes however, are additive because G is a state function : ΔG∘3=ΔG∘1+ΔG∘2
If number of electrons in the reacton are n1,n2 and n2 respectively, then standard electrode potential of reation (3) isAE∘3=n1E∘1+n2E∘2n3BE∘3=n1E∘1−n2E∘2n3CE∘3=(E1−E2)D−E∘3=(E1+E2)
If E1andE2 are two events and E2 is a subset of E1 then P(E1/E2)=_____
View SolutionRead the following passage for the evaluation of E∘ when different number of electrons are involved. Consider addition of the following half reactions
(1) Fe3+(aq)+3e−→Fe(s)E∘1=0.45V
(2) Fe(s)→Fe2+(aq)+2e−E∘2=−0.04V
(3) Fe3+(aq)+e−→Fe2+(aq)E∘3=?
Because half-reactions (1) and (2) contains a different number of electrons, the net reaction (3) is another half-reaction and E∘3 can't be obtained simply by adding E∘1 and E∘3. The free - energy changes however, are additive because G is a state function : ΔG∘3=ΔG∘1+ΔG∘2
Standard electrode potential for the half-cell Fe3+/Fe2+ of the reaction (3) is :View SolutionRead the following passage for the evaluation of E∘ when different number of electrons are involved. Consider addition of the following half reactions
(1) Fe3+(aq)+3e−→Fe(s)E∘1=0.45V
(2) Fe(s)→Fe2+(aq)+2e−E∘2=−0.04V
(3) Fe3+(aq)+e−→Fe2+(aq)E∘3=?
Because half-reactions (1) and (2) contains a different number of electrons, the net reaction (3) is another half-reaction and E∘3 can't be obtained simply by adding E∘1 and E∘3. The free - energy changes however, are additive because G is a state function : ΔG∘3=ΔG∘1+ΔG∘2
For the reactions
(1) MnO−4+8H++5e−→Mn2+4H2O
E∘=1.51V
(2) MnO2+4H++2e−→Mn2+2H2O
E∘=1.32 then for the reaction
(3) MnO−4+4H++3e−→MnO2+2H2O,E∘ isView SolutionA hydrogen electrode placed in a buffer solution of CH3COONa and CH3COOH in the ratios of x:y and y:x has electrode potential values E1 volts and E2 volts, respectively at 25∘C The pKa values of acetic acid is (E1 and E2 are oxidation potential)
View SolutionConsider the following E1/SN1 reaction :
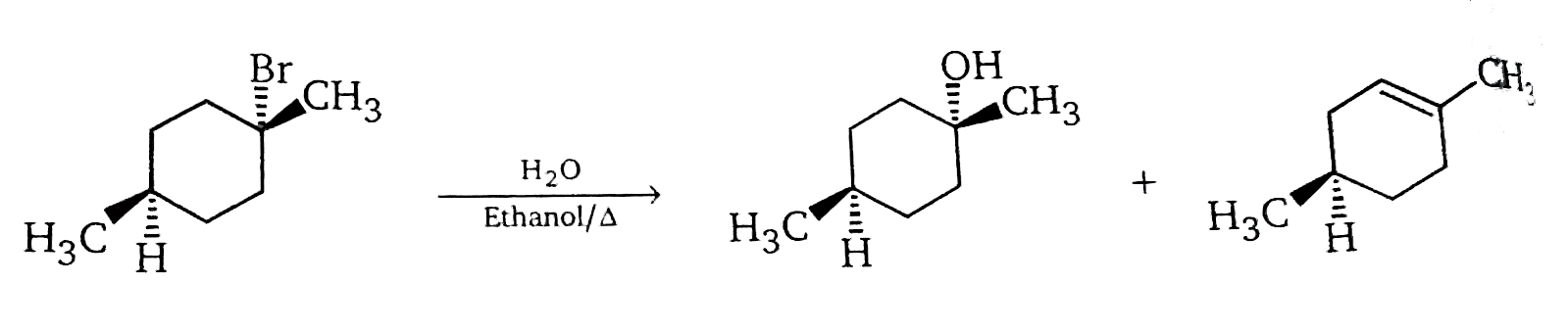
the missing prduct (a) is (are):
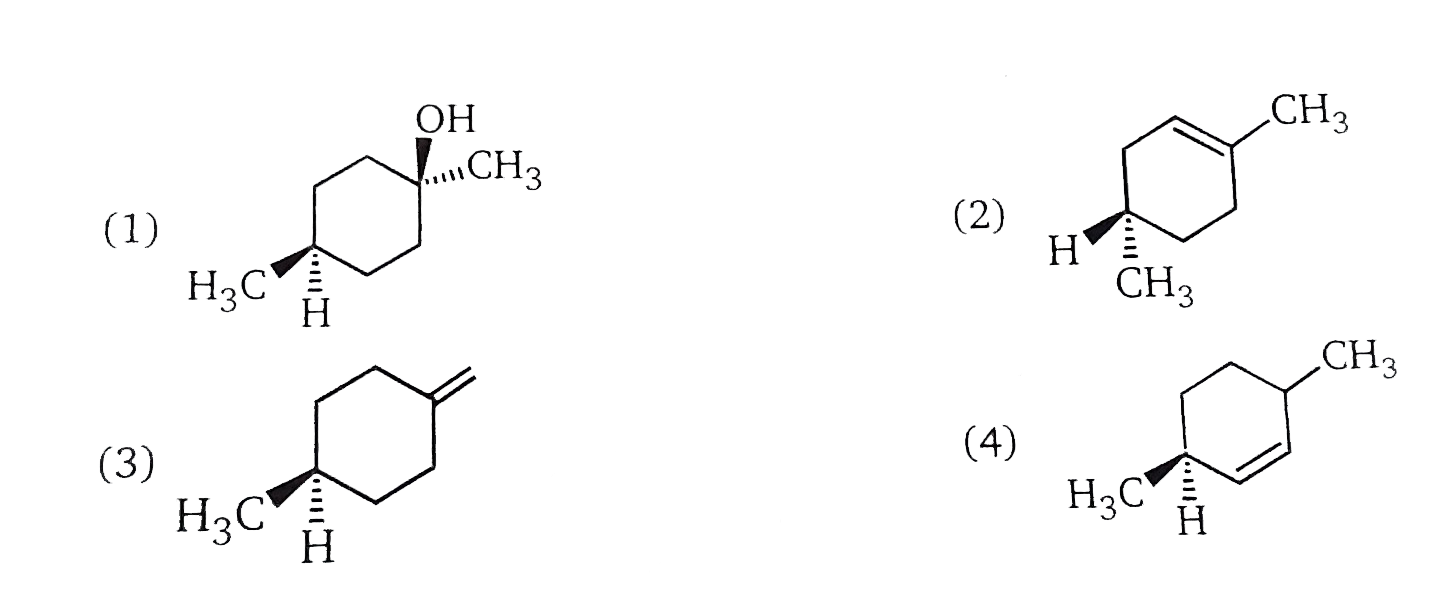 View Solution
View Solution

