A beam of 450 nm light is incident on a metal having work function 2eV and placed in a magnetic field B. If the most energetic electrons emitted are bent into circular are of radius 0.2 m, find B.
2.36×10−4T
1.46×10−5 T
6.9×10−5T
9.2×10−6T
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Calculate the energy of the incident light
The energy of a photon can be calculated using the formula:
E=hcλ
where:
- h = Planck's constant = 4.14×10−15eV s
- c = speed of light = 3×108m/s
- λ = wavelength of light = 450nm=450×10−9m
Substituting the values:
E=(4.14×10−15eV s)(3×108m/s)450×10−9m=2.76eV
Step 2: Calculate the maximum kinetic energy of the emitted electrons
Using Einstein's photoelectric equation:
Kmax=E−ϕ
where ϕ is the work function of the metal (given as 2eV):
Kmax=2.76eV−2eV=0.76eV
Step 3: Convert kinetic energy to joules
To convert the kinetic energy from eV to joules, we use:
Kmax=0.76eV×1.6×10−19J/eV=1.216×10−19J
Step 4: Calculate the maximum velocity of the emitted electrons
Using the kinetic energy formula:
Kmax=12mv2
Rearranging for v:
v=√2Kmaxm
where m is the mass of an electron (9.1×10−31kg):
v=√2×1.216×10−19J9.1×10−31kg=0.52×106m/s
Step 5: Calculate the magnetic field
The radius r of the circular path of the electrons in a magnetic field is given by:
r=mveB
Rearranging for B:
B=mver
Substituting the known values:
- e=1.6×10−19C
- r=0.2m
B=(9.1×10−31kg)(0.52×106m/s)(1.6×10−19C)(0.2m)
Calculating B:
B=4.732×10−253.2×10−20=1.48×10−5T
Final Answer
Thus, the magnetic field B is approximately:
B≈1.46×10−5T
The energy of a photon can be calculated using the formula:
E=hcλ
where:
- h = Planck's constant = 4.14×10−15eV s
- c = speed of light = 3×108m/s
- λ = wavelength of light = 450nm=450×10−9m
E=(4.14×10−15eV s)(3×108m/s)450×10−9m=2.76eV
Using Einstein's photoelectric equation:
Kmax=E−ϕ
where ϕ is the work function of the metal (given as 2eV):
Kmax=2.76eV−2eV=0.76eV
To convert the kinetic energy from eV to joules, we use:
Kmax=0.76eV×1.6×10−19J/eV=1.216×10−19J
Using the kinetic energy formula:
Kmax=12mv2
Rearranging for v:
v=√2Kmaxm
where m is the mass of an electron (9.1×10−31kg):
v=√2×1.216×10−19J9.1×10−31kg=0.52×106m/s
The radius r of the circular path of the electrons in a magnetic field is given by:
r=mveB
Rearranging for B:
B=mver
Substituting the known values:
- e=1.6×10−19C
- r=0.2m
B=4.732×10−253.2×10−20=1.48×10−5T
Thus, the magnetic field B is approximately:
B≈1.46×10−5T
Topper's Solved these Questions
- BOOK - MTG-WBJEECHAPTER - PARTICLE NATURE OF LIGHT AND WAVE PARTICLE DUALISMEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS15videos
PARTICLE NATURE OF LIGHT AND WAVE PARTICLE DUALISM
- BOOK - MTG-WBJEECHAPTER - OSCILLATIONS AND WAVESEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))2videos
OSCILLATIONS AND WAVES
- BOOK - MTG-WBJEECHAPTER - SOLID STATE ELECTRONS EXERCISE - WB JEE Previous Years Questions (CATEGORY 1 : Single Option Correct Type)15videos
SOLID STATE ELECTRONS
Similar Questions
A beam of 450 nm light is incident on a metal having work function 2.0 eV and placed in a magnetic field B. The most energetic electrons emitted perpendicular to the field are bent in circular arcs of radius 20 cm. Find the value of B.
View Solution(a) A beam of 450 nm light is incident on a metal having work function 2.0eV and placed in a magnetic field B. The most energetic electron emitted perpendicular to the field are bent in circular are of radius 20 cm. Find the value of B.
(b) A small plate of metal (work function =1.17eV) is placed at a distance of 2 m from a monochromatic light source of wavelength 4.8×10−7 m and power 1.0W. The light falls normally on the plate. Find the number of photons striking the metal plate per square meter per second. If a constant uniform magnetic field of strength 10−4 T is applied parallel to the metal surface, find the radius of the largest circular path following by the emitted photoelectrons.View Solution
Knowledge Check
- Question 1 - Select One
A beam of light of wavelength λ is incident on a metal having work function ϕ and placed on a metal having work function ϕ and placed in a magnetic field B. The most energetic electrons emitted perpendicular to the field are bent in circular arcs of radius R. Then
AB=mveR, where hcλ=ϕ+12mv2BB=mReV, where hcλ=ϕ+12mv2CB=mveR, where hcλ+ϕ=12mv2Dnone - Question 2 - Select One
Light of wavelength 500nm is incident on a metal with work function 2.28eV. The de Broglie wavelength of the emitted electron is
A≤2.8×10−12mB<2.8×10−10mC<2.8×10−9mD≥2.8×10−9m - Question 3 - Select One
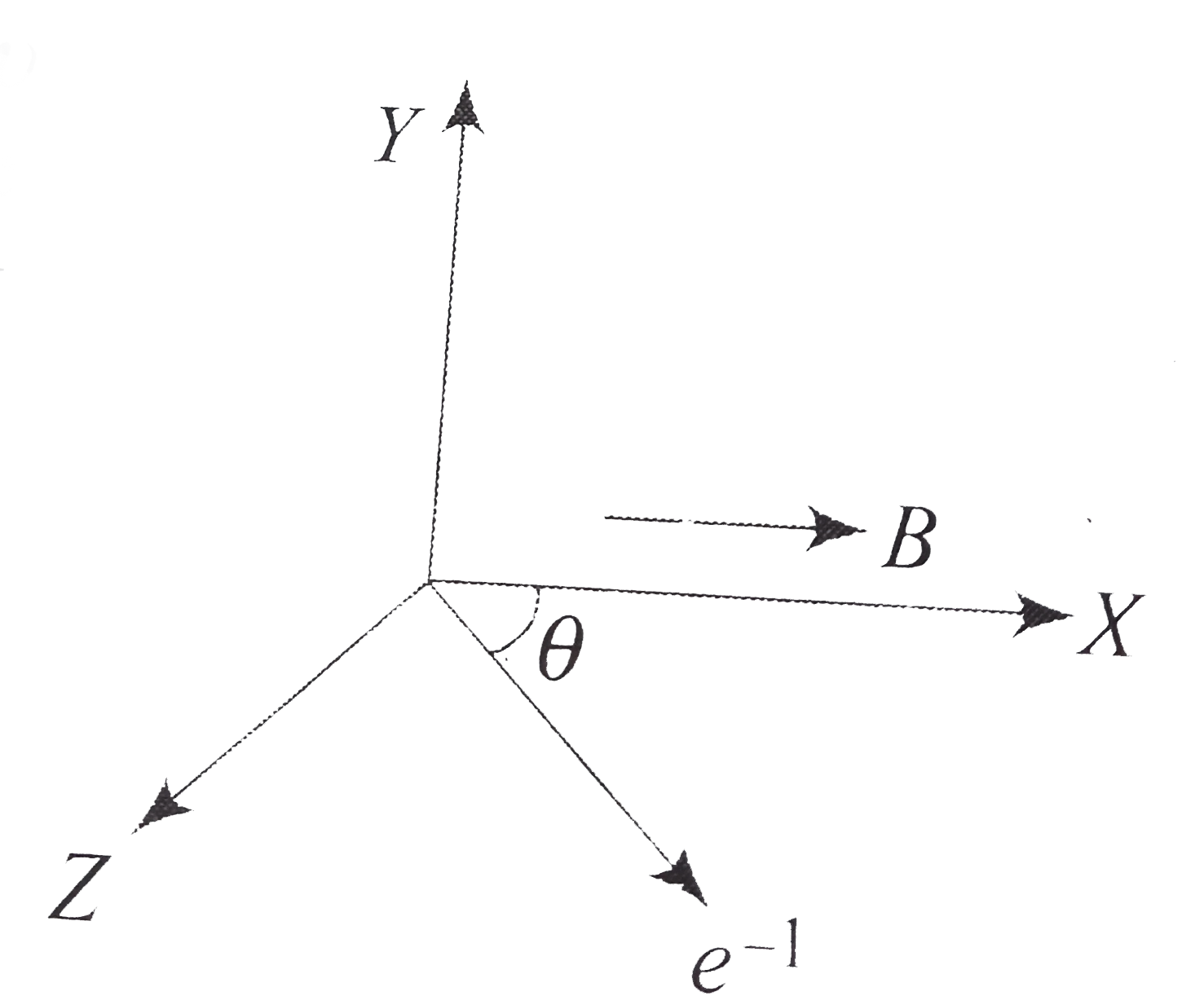
Light having photon energy hυ is incident on a metallic plate having work function ϕ to eject the electrons. The most energetic enectrons are then allowed to enter in a region of uniform magnetic field B as shown in Fig. The electrons are projected In X-Z plane making an angle θ with X-axis and magnetic field is →B=B0ˆi along X-axis maximum pitch of the helix described by an electron is found to be p. Take mass of electron as m and charge as q. Based on the above information, answer the following questions:
Q. The plot between X-coordinate of the location of electron as a function of time for different frequencies υ of the incident light isA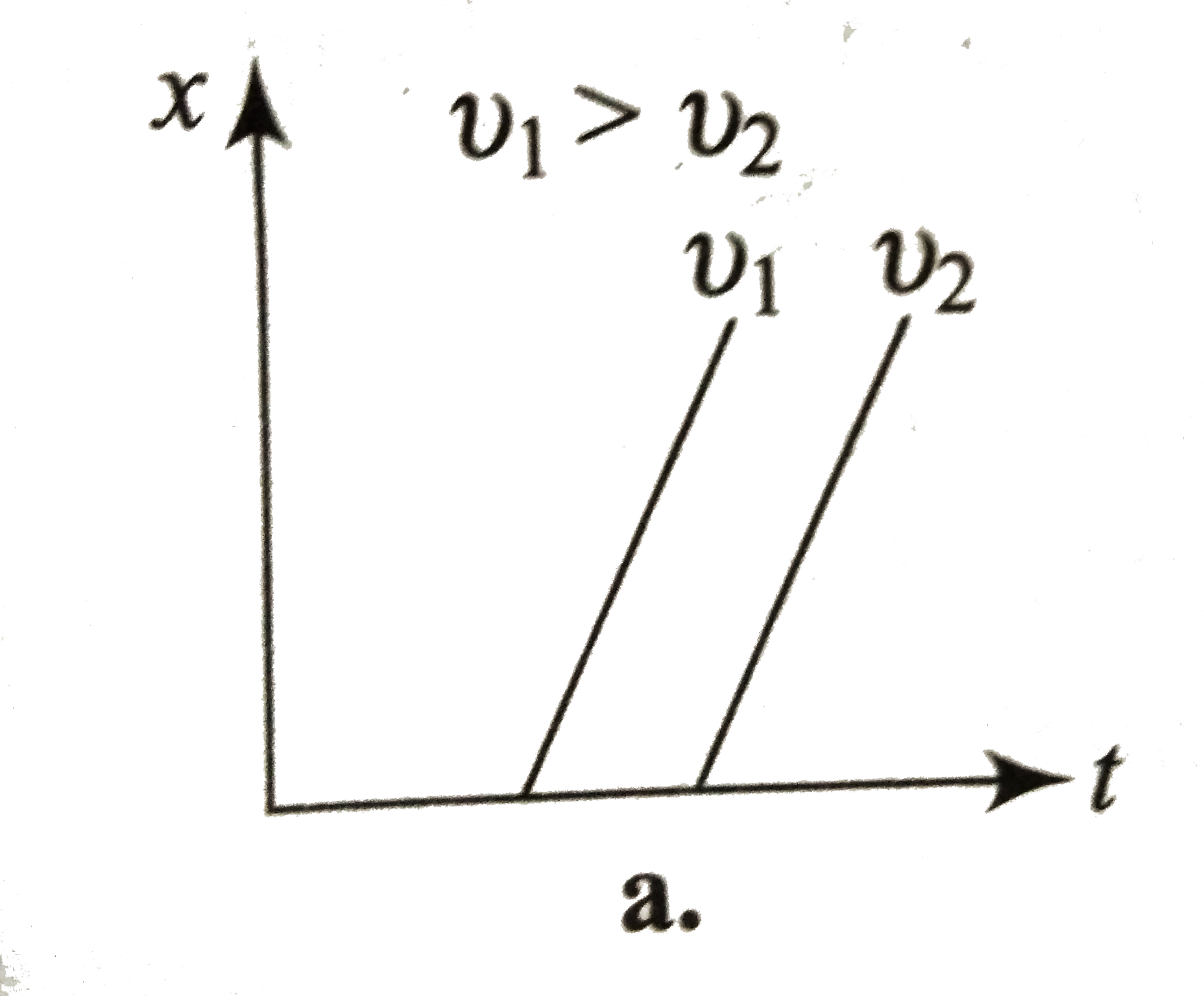 B
B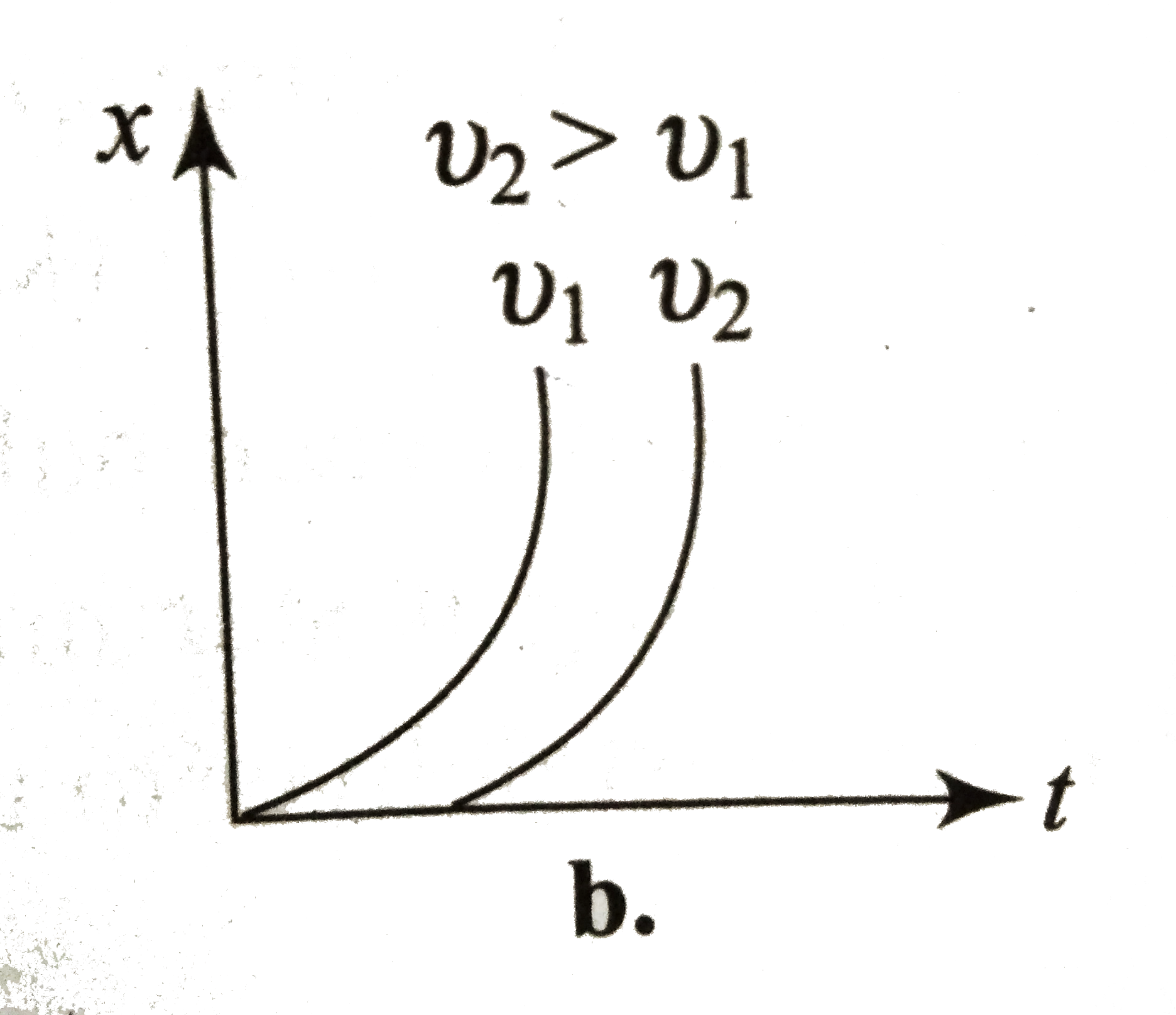 C
C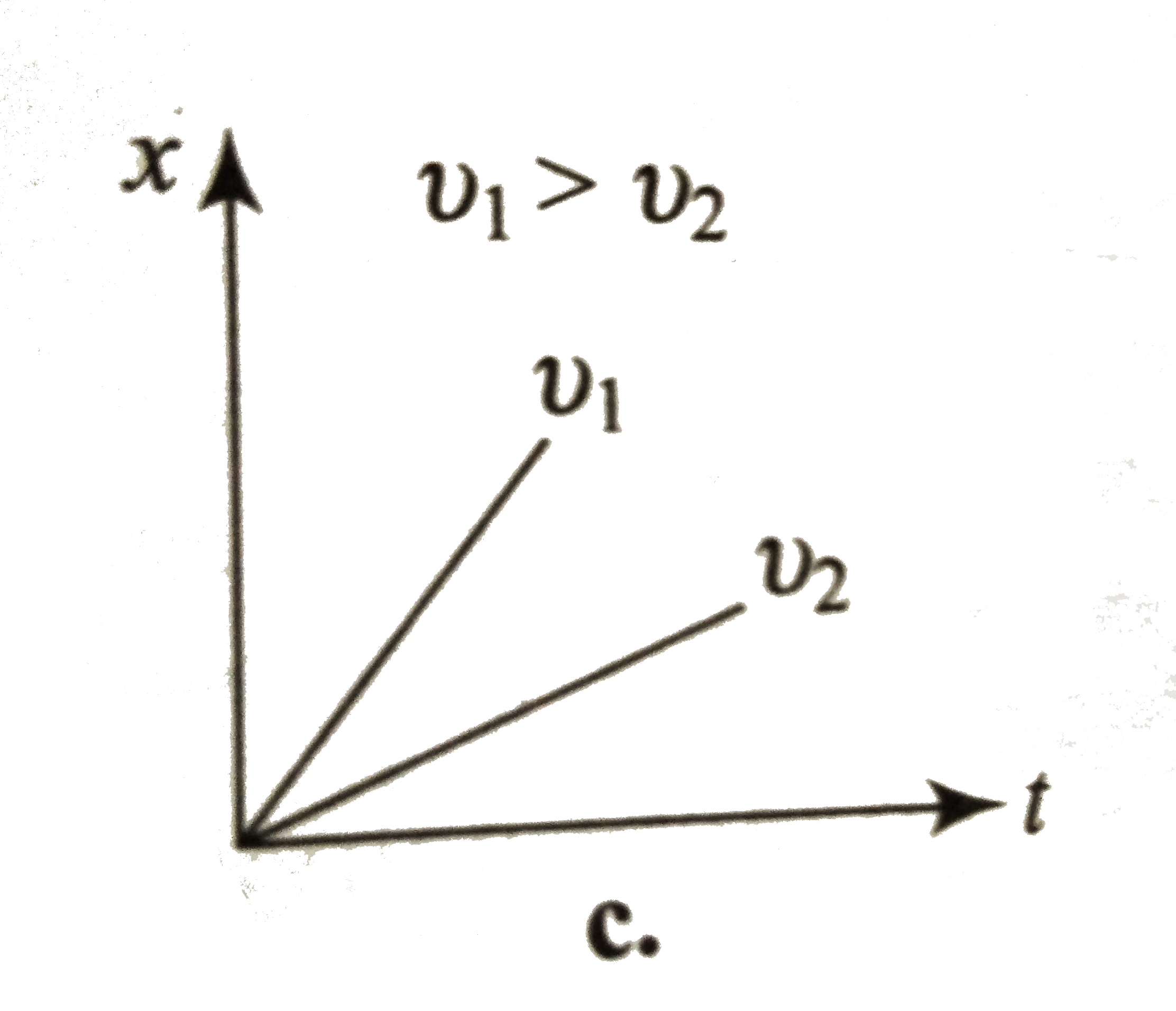 D
D
A light beam of wavelength 500 nm is incident on a metal having work function of 1.25 eV, placed in a magnetic field of intensity B. The electrons emitted perpendicular to the magnetic field B, with maximum kinetic energy are bent into circular arc of radius 30 cm. The value of B is ______×10−7T.
Given hc=20×10−26 J-m , mass of electron =9×10−31 kgView SolutionLight of 5,500Å is incident on a metal of work function 2 eV . Calculate the
(i) threshold wavelength
(ii) maximum velocity of electrons emitted.View Solution
Light having photon energy hυ is incident on a metallic plate having work function ϕ to eject the electrons. The most energetic enectrons are then allowed to enter in a region of uniform magnetic field B as shown in Fig. The electrons are projected In X-Z plane making an angle θ with X-axis and magnetic field is →B=B0ˆi along X-axis maximum pitch of the helix described by an electron is found to be p. Take mass of electron as m and charge as q. Based on the above information, answer the following questions:
Q. Considering the instant of crossing origin at t=0 ,the Z-coordinate of the location of electron as a function of time isView SolutionLight of waelength 4000Å is incident on a metal plate with work function 2eV. The max. K.E. of the photoelectrons is
View Solution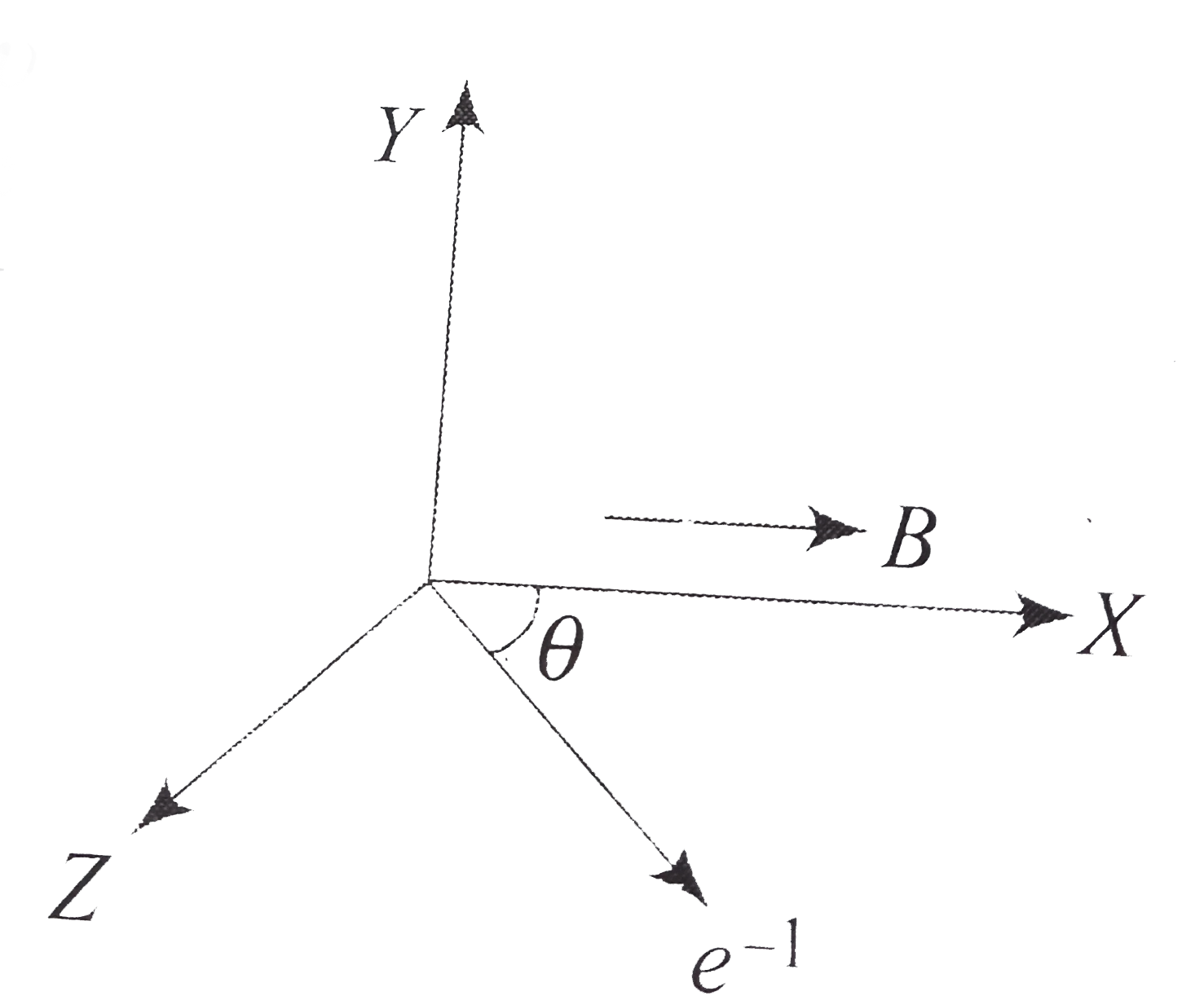
Light having photon energy hυ is incident on a metallic plate having work function ϕ to eject the electrons. The most energetic enectrons are then allowed to enter in a region of uniform magnetic field B as shown in Fig. The electrons are projected In X-Z plane making an angle θ with X-axis and magnetic field is →B=B0ˆi along X-axis maximum pitch of the helix described by an electron is found to be p. Take mass of electron as m and charge as q. Based on the above information, answer the following questions:
Q. The correct relation between p and B0 isView Solution

