D, E and F are respectively the mid-points of sides AB. BC and CA of $Δ A B C$ . Find the ratio of the areas of DDEF and $Δ A B C$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $1 : 4$

Answer

Step by step video & text solution for D, E and F are respectively the mid-points of sides AB. BC and CA ofDeltaA B C . Find the ratio of the areas of DDEF andDeltaA B C . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

BOOK - VK GLOBAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - PROFICIENCY EXERCISE (LONG ANSWER QUESTIONS)
15videos
TRIANGLES
BOOK - VK GLOBAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - SELF ASSESSMENT TEST
10videos
TRIANGLES
BOOK - VK GLOBAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - PROFICIENCY EXERCISE (VERY SHORT ANSWER QUESTIONS)
14videos
TRIANGLES
BOOK - VK GLOBAL PUBLICATIONCHAPTER - REAL NUMBERSEXERCISE - Self -Assessment Test
11videos
REAL NUMBERS
BOOK - VK GLOBAL PUBLICATIONCHAPTER - VALUE-BASED QUESTIONSEXERCISE - Unit-VII : (Statistics & Probability)
8videos
VALUE-BASED QUESTIONS

Knowledge Check

Question 1 - Select One
If D, E and F are the mid-points of sides BC, CA and AB respectively of $△ A B C$ , then the ratio of the areas of $△ D E F$ to the area of $△ A B C$ is :
A $1 : 4$
B $1 : 2$
C $1 : 3$
D $2 : 3$

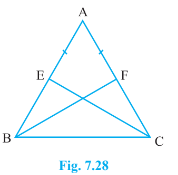
E and F are respectively the mid-points of equal sides AB and AC of $Δ A B C$ (see Fig. 7.28). Show that BF = C E.

View Solution
D, E and F are respectively the mid -points of the sides BC, CA and AB of a $△ A B C$ .Show that (i) BDEF is a parallelogram
View Solution
D, E and F are respectively the mid-points of the sides BC, CA and AB of a $Δ A B C$ . Show that
ar(BDEF) = $\frac{1}{2} a r (△ A B C)$
View Solution
In $Δ A B C$ , D, E and F are respectively the mid-points of sides AB, BC and CA. Show that $Δ A B C$ is divided into four congruent triangles by joining D, E and F.
View Solution
$D, E, F$ are the mid-points of the sides $B C, C A$ and $A B$ respectively of a $A B C$ . Determine the ratio of the areas of $D E F$ and $A B C$ .
View Solution
D, E and F are respectively the mid-points of the sides BC, CA and AB of a $Δ A B C$ . Show that
$a r (△ D E F) = \frac{1}{4} a r (△ A B C)$
View Solution
D, E and F are respectively the mid-points of the sides BC, CA and AB of a $Δ A B C$ .Show that (i) BDEF is a parallelogram. (ii) $a r (D E F) = \frac{1}{4} a r (A B C)$ (iii) $a r (B D E F) = \frac{1}{2} a r (A B C)$
View Solution

VK GLOBAL PUBLICATION-TRIANGLES-PROFICIENCY EXERCISE (SHORT ANSWER TYPE QUESTIONS-II)

A street light bulb is fixed on a pole 6 m above the level of the stre...
03:22
In Fig.7.70, find angleE.
05:53
D, E and F are respectively the mid-points of sides AB. BC and CA o...
05:39
A 15 high tower casts a sshadow 24 long at a certain time at the same ...
03:17
Prove that the sum of the squares of the sides of a rhombus is equa...
05:22
In Fig. 3, ABC is a right triangle, right angled at C and D is the mi...
02:39
In Fig, ABC is an isosceles triangle in which AB= AC.Eis a point on th...
02:02
A D is an altitude of an equilateral triangle A B Cdot On A D as base,...
03:00
In figure, P is the mid-point of B C ,Q is the mid-point of B C ,Q is ...
04:28
AB botBC and DE bot AC. Prove that DeltaABC ~ DeltaAED.
01:20
Two triangles B A Ca n dB D C , right angled at Aa n dD respectively, ...
02:17
E is a point on side A D produced of a parallelogram A B C D and...
01:41
D and E are respectively the points on the sides AB and AC of a triang...
05:02
If ABC is an equilateral triangle with each side a cm such that ADbotB...
04:09
In A B C ,\ \ D E is parallel to base B C , with D on A B and E on...
02:55
If E is a point on side r:A of an equilateral triangle ABC such that B...
05:26
O is any point inside a rectangle ABCD. Prove that O B^2+O D^2=O A^2+...
03:16
In the given figure, (AD)/(DB)=(AE)/(EC) and angle ADE=angleACB. Prov...
02:02
In Fig. 4.72, A B C D . If O A=3x-19 ,\ \ O B=x-4 , O C=x-3 and O ...
02:08
A B C is a triangle and P Q is a straight line meeting A B in P ...
02:53

Home
Ask Doubt
Profile

D, E and F are respectively the mid-points of sides AB. BC and CA ofΔABC . Find the ratio of the areas of DDEF andΔABC .

The correct Answer is:1:4

Topper's Solved these Questions

Similar Questions

Knowledge Check

If D, E and F are the mid-points of sides BC, CA and AB respectively of △ABC, then the ratio of the areas of △DEF to the area of △ABC is :

VK GLOBAL PUBLICATION-TRIANGLES-PROFICIENCY EXERCISE (SHORT ANSWER TYPE QUESTIONS-II)

D, E and F are respectively the mid-points of sides AB. BC and CA of $Δ A B C$ . Find the ratio of the areas of DDEF and $Δ A B C$ .

The correct Answer is: $1 : 4$

If D, E and F are the mid-points of sides BC, CA and AB respectively of $△ A B C$ , then the ratio of the areas of $△ D E F$ to the area of $△ A B C$ is :