PQL and PRM are tangents to a circle with centre O at points Q and R respectively. S is a point on the circle such that ∠SQL=50∘ and ∠SRM=60∘. Find value of ∠QSR.
The correct Answer is:70∘
Step by step video, text & image solution for PQL and PRM are tangents to a circle with centre O at points Q and R respectively. S is a point on the circle such that angleSQL=50^@ and angleSRM=60^@. Find value of angleQSR. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLES BOOK - VK GLOBAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - PROFICIENCY EXERCISE (Long Answer Questions 4 mark)
12 Videos
- CIRCLES BOOK - VK GLOBAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - SELF - ASSESSMENT TEST
11 Videos
- CIRCLES BOOK - VK GLOBAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - PROFICIENCY EXERCISE (Short Answer Questions - I 2 mark)
13 Videos
- ARITHMETIC PROGRESSIONS BOOK - VK GLOBAL PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - SELF ASSESSMENT TEST
10 Videos
- COORDINATE GEOMETRY BOOK - VK GLOBAL PUBLICATIONCHAPTER - COORDINATE GEOMETRY EXERCISE - SELF-ASSESSMENT TEST
10 Videos
Similar Questions
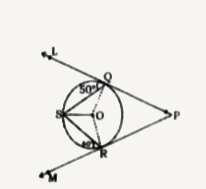
PQL and PRM are tangents to a circle with centre O at points Q and R respectively. S is a point on the circle such that ∠SQL=50∘ and ∠SRM=60∘. Find value of ∠QSR.
View SolutionIn the given figure, PQL and PRM are tangents to the circle with centre 'O' at the points Q and R, respectively and S is a point on the circle such that ∠SQL=50∘and∠SRM=60∘. Then ∠QSR is equal to
View Solution
Knowledge Check
In the figure, O is the centre of a circle,PQL and PRM are the tangents at the points Q and R respectively and Sis a point on the circle such that ∠SQL=50∘and∠SRM=60∘. Then , ∠QSR is equal to
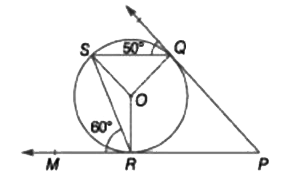 A40∘B50∘C60∘D70∘
A40∘B50∘C60∘D70∘In the figure , PQ and PR are tangent to the circle with centre O. Also, S is a point on the circle such that ∠SQC=50∘and∠SRM=60∘, then ∠QSR=
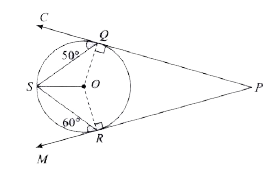 A40∘B70∘C80∘D45∘
A40∘B70∘C80∘D45∘PA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=100∘ , then OAB is equal to:
A25∘B20∘C35∘D50∘
In Figure, XPandXQ are tangents from X to the circle with centre O.R is a point on the circle. Prove that, XA+AR=XB+BR
View SolutionAP is tangent to the circle with centre O at point A. OP =10 cm and ∠OPA=30∘. The radiu of the circle is
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=40∘, then ∠OABis equal to:
View SolutionIn figure , APB is a tangent to a circle with centre O at point, If ∠QPB=50∘ , then the measure of ∠POQ is
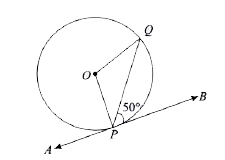
View SolutionPA and PB are tangents to a circle with centre O, from a point P outside the circle and A and B are points on the circle. If ∠APB=30∘, then ∠OAB is equal to :
View Solution
