A is a point at a distance 10 cm from the centre O of a circle of radius 6cm . AP and AQ are the tangents to the circle at P and Q .If a tangent BC is drawn at a point R lying on the mirror are PQ to intersect AP at B and AQ at C, find the perimeter of the ΔABC .
The correct Answer is:16 cm
To find the perimeter of triangle ABC, we will follow these steps:
Step 1: Understand the Configuration
We have a circle with center O and radius 6 cm. Point A is located 10 cm away from O. From point A, we draw two tangents AP and AQ to the circle, touching the circle at points P and Q respectively.
Step 2: Identify the Right Triangle
Since the radius of the circle is perpendicular to the tangent at the point of tangency, triangle OAP is a right triangle where:
- OA = 10 cm (distance from center to point A)
- OP = 6 cm (radius of the circle)
Step 3: Apply the Pythagorean Theorem
Using the Pythagorean theorem in triangle OAP:
OA2=OP2+AP2
Substituting the known values:
102=62+AP2
100=36+AP2
AP2=100−36=64
AP=√64=8 cm
Step 4: Find the Length of AQ
Since AP and AQ are tangents from point A to the circle, they are equal in length:
AQ=AP=8 cm
Step 5: Identify the Lengths of Tangents from R
Let R be a point on the minor arc PQ. The tangent BC drawn at point R intersects AP at B and AQ at C. By the properties of tangents from a point outside the circle:
- BP = BR
- CQ = CR
Step 6: Calculate the Perimeter of Triangle ABC
The perimeter of triangle ABC can be expressed as:
Perimeter=AB+BC+AC
We can express BC as:
BC=BR+CR
Since BP = BR and CQ = CR, we can substitute:
BC=BP+CQ
Thus, the perimeter becomes:
Perimeter=AB+BP+CQ+AC
Since AB = AP = 8 cm and AC = AQ = 8 cm, we have:
Perimeter=8+BP+8+CQ
Since BP = CQ (as they are tangents from the same external point R), we can denote them as x:
Perimeter=8+x+8+x=16+2x
However, since we are looking for the perimeter of triangle ABC and we have already established that both tangents from point A are equal, we can conclude:
Perimeter=16 cm
Final Answer
The perimeter of triangle ABC is 16 cm.
---
We have a circle with center O and radius 6 cm. Point A is located 10 cm away from O. From point A, we draw two tangents AP and AQ to the circle, touching the circle at points P and Q respectively.
Since the radius of the circle is perpendicular to the tangent at the point of tangency, triangle OAP is a right triangle where:
- OA = 10 cm (distance from center to point A)
- OP = 6 cm (radius of the circle)
Using the Pythagorean theorem in triangle OAP:
OA2=OP2+AP2
Substituting the known values:
102=62+AP2
100=36+AP2
AP2=100−36=64
AP=√64=8 cm
Since AP and AQ are tangents from point A to the circle, they are equal in length:
AQ=AP=8 cm
Let R be a point on the minor arc PQ. The tangent BC drawn at point R intersects AP at B and AQ at C. By the properties of tangents from a point outside the circle:
- BP = BR
- CQ = CR
The perimeter of triangle ABC can be expressed as:
Perimeter=AB+BC+AC
We can express BC as:
BC=BR+CR
Since BP = BR and CQ = CR, we can substitute:
BC=BP+CQ
Thus, the perimeter becomes:
Perimeter=AB+BP+CQ+AC
Since AB = AP = 8 cm and AC = AQ = 8 cm, we have:
Perimeter=8+BP+8+CQ
Since BP = CQ (as they are tangents from the same external point R), we can denote them as x:
Perimeter=8+x+8+x=16+2x
However, since we are looking for the perimeter of triangle ABC and we have already established that both tangents from point A are equal, we can conclude:
Perimeter=16 cm
The perimeter of triangle ABC is 16 cm.
Topper's Solved these Questions
- CIRCLES BOOK - VK GLOBAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - SELF - ASSESSMENT TEST
11 Videos
- CIRCLES BOOK - VK GLOBAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - PROFICIENCY EXERCISE (Short Answer Questions - II 3 mark)
22 Videos
- ARITHMETIC PROGRESSIONS BOOK - VK GLOBAL PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - SELF ASSESSMENT TEST
10 Videos
- COORDINATE GEOMETRY BOOK - VK GLOBAL PUBLICATIONCHAPTER - COORDINATE GEOMETRY EXERCISE - SELF-ASSESSMENT TEST
10 Videos
Similar Questions
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at Band AQ at C, find the perimeter of the ΔABC
View SolutionA is a point at a distance 26 cm from the centre O of a circle of radius 10 cm. AP and AQ are the tangents to the circle at the point of contacts P and Q. If a tangent BC is drawn at a point R lying on the minor are PQ to intersect AP at B and AQ at C, then the perimeter of △ABC is:
त्रिज्या 10 सेमी के वृत्त के केंद्र O से 26 सेमी की दूरी पर A एक बिंदु है। AP और AQ बिंदु P और Q पर स्पर्शरेखा है। यदि स्पर्शरेखा BC वृत्त के PQ माइनर को R पर कटती है और PA को B पर और PQ को C पर प्रतिछेदित करती है , तो ABC की परिधि है
View SolutionA is a point at a distance 26 cm from the centre O of a circle of radius 10 cm. AP and AQ are the tangents to the circle at the point of contacts P and Q. If a tangent BC is drawn at a point R lying on the minor are PQ to intersect AP at B and AQ at C, then the perimeter of △ABC is:
त्रिज्या 10 सेमी के वृत्त के केंद्र O से 26 सेमी की दूरी पर A एक बिंदु है। AP और AQ बिंदु P और Q पर स्पर्शरेखा हैं। यदि स्पर्शरेखा BC वृत्त के PQ माइनर को R पर कटती है और PA को B पर और PQ को C पर प्रतिछेदित करती है , तो ABC की परिधि है
View SolutionA point P is at a distance of 29cm from the centre of a circle of radius 20cm. Find the length of the tangent drawn from P to the circle.
View SolutionIf a point P is 17 cm from the centre of a circle of radius 8 cm, then find the length of the tangent drawn to the circle from point P.
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm . Find the radius of the circle.

View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
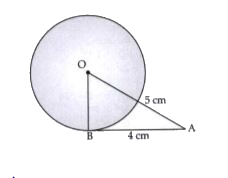
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
View SolutionFrom a point P which is at a distance of 13 cm form the centre of the circle of radius 5 cm, a tangent is drawn to the circle . The length of the tangent is ____________
View SolutionA line through the centre O of a circle of radius 7 cm cuts the tangent, at a point P on the circle, at Q such that PQ=24cm . Find OQ .
View Solution
