Find the area of the flower bed (with semicircular ends). 
The correct Answer is:(704+64π)cm2
Step by step video, text & image solution for Find the area of the flower bed (with semicircular ends). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS RELATED TO CIRCLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Proficiency Exercise (Long Answer Questions)
19 Videos
- AREAS RELATED TO CIRCLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Self -Assessment Test
11 Videos
- AREAS RELATED TO CIRCLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Proficiency Exercise (Short Answer Questions -I)
13 Videos
- ARITHMETIC PROGRESSIONS BOOK - VK GLOBAL PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - SELF ASSESSMENT TEST
10 Videos
Similar Questions
Knowledge Check
A solid cylinder has total surface area of 462 sq. cm. Its curved surface area is 13rd of the total surface area. Then the radius of the cylinder is
Aπ:(π+2)B(π+2):πC1:1Dnone of these
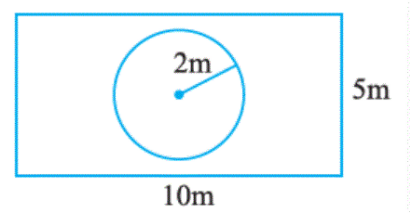
The adjoining figure represents a rectangular lawn with a circular flower bed in the middle. Find:
(i) the area of the whole land
(ii) the area of the flower bed
(iii) the area of the lawn excluding the area of the flower bed
(iv) the circumference of the flower bed.
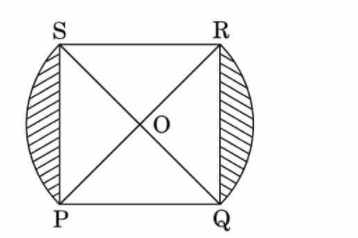
View Solution. In the following figure, PQRS is square lawn with side PQ = 42 metres. Two circular flower beds are there on the sides PS and QR with centre at O, the intersections of its diagonals. Find the total area of the two flower beds (shaded parts).
View SolutionEach side of a square flower bed is 2 m 80 cm long. It is extended by digging a strip 30 cm wide all around it. Find the area of the enlarged flower bed and also the increase in the area of the flower bed.
View SolutionEach side of a square flower bed is 2 m 80 cm long. It is extended by digging a strip 30 cm wide all around it. Find the area of the enlarged flower bed and also the increase in the area of the flower bed.
View SolutionThe given quantity of metal is to be cost into a half cylinder with a rectangular base and semicircular ends. Show that in order that the total surface area may be minimum, the ratio of the length of the cylinder to the diameter of its semi-circular ends is π:(π+2).
View Solution40. A given quantity of metal is to be cast into a half cylinder with a rectangular base and semicircular ends. Show that in order that the total surface area may be minimum, the ratio of the length of the cylinder to the diameter of its semi-circular ends is w (
View SolutionFind the centre of mass of a uniform semicircular ring of radius R and mass M.
View Solution


