Find the mean, mode and median for the following data :
ClassFrequency0−10 810−20 1620−30 3630−40 3440−50 6Total 100
The correct Answer is:=29.09
To find the mean, mode, and median for the given frequency distribution data, we will follow these steps:
Step 1: Create a Frequency Distribution Table
We will organize the given data into a frequency distribution table, including cumulative frequency.
| Class Interval | Frequency (f) | Cumulative Frequency (cf) |
|----------------|---------------|---------------------------|
| 0 - 10 | 8 | 8 |
| 10 - 20 | 16 | 24 |
| 20 - 30 | 36 | 60 |
| 30 - 40 | 34 | 94 |
| 40 - 50 | 6 | 100 |
| Total | 100 | |
Step 2: Find the Median
To find the median, we need to determine the median class.
1. Calculate n/2:
- Total frequency (n) = 100
- n/2 = 100/2 = 50
2. Identify the Median Class:
- The cumulative frequency just greater than 50 is 60, which corresponds to the class interval 20 - 30.
3. Use the Median Formula:
- Median =L+(n/2−cf)f×H
- Where:
- L=20 (lower limit of the median class)
- n/2=50
- cf=24 (cumulative frequency of the class before median class)
- f=36 (frequency of the median class)
- H=10 (class width)
Plugging in the values:
Median=20+(50−24)36×10
=20+2636×10
=20+7.22≈27.22
Step 3: Find the Mode
To find the mode, we need to identify the modal class and use the mode formula.
1. Identify the Modal Class:
- The class with the highest frequency is 20 - 30 (frequency = 36).
2. Use the Mode Formula:
- Mode =L+(f1−f0)(2f1−f0−f2)×H
- Where:
- L=20 (lower limit of the modal class)
- f1=36 (frequency of modal class)
- f0=16 (frequency of the class before modal class)
- f2=34 (frequency of the class after modal class)
- H=10 (class width)
Plugging in the values:
Mode=20+(36−16)(2×36−16−34)×10
=20+2072−50×10
=20+2022×10
=20+9.09≈29.09
Step 4: Find the Mean
To find the mean, we use the formula:
Mean=∑(f⋅x)n
Where x is the midpoint of each class.
1. Calculate Midpoints:
- For class 0-10: x=5
- For class 10-20: x=15
- For class 20-30: x=25
- For class 30-40: x=35
- For class 40-50: x=45
2. Calculate f⋅x:
- 8⋅5=40
- 16⋅15=240
- 36⋅25=900
- 34⋅35=1190
- 6⋅45=270
3. Sum of f⋅x:
∑(f⋅x)=40+240+900+1190+270=2640
4. Calculate Mean:
Mean=2640100=26.4
Final Results
- Mean: 26.4
- Median: 27.22
- Mode: 29.09
We will organize the given data into a frequency distribution table, including cumulative frequency.
|----------------|---------------|---------------------------|
| 0 - 10 | 8 | 8 |
| 10 - 20 | 16 | 24 |
| 20 - 30 | 36 | 60 |
| 30 - 40 | 34 | 94 |
| 40 - 50 | 6 | 100 |
| Total | 100 | |
To find the median, we need to determine the median class.
- Total frequency (n) = 100
- n/2 = 100/2 = 50
- The cumulative frequency just greater than 50 is 60, which corresponds to the class interval 20 - 30.
- Median =L+(n/2−cf)f×H
- Where:
- L=20 (lower limit of the median class)
- n/2=50
- cf=24 (cumulative frequency of the class before median class)
- f=36 (frequency of the median class)
- H=10 (class width)
Median=20+(50−24)36×10
=20+2636×10
=20+7.22≈27.22
To find the mode, we need to identify the modal class and use the mode formula.
- The class with the highest frequency is 20 - 30 (frequency = 36).
- Mode =L+(f1−f0)(2f1−f0−f2)×H
- Where:
- L=20 (lower limit of the modal class)
- f1=36 (frequency of modal class)
- f0=16 (frequency of the class before modal class)
- f2=34 (frequency of the class after modal class)
- H=10 (class width)
Mode=20+(36−16)(2×36−16−34)×10
=20+2072−50×10
=20+2022×10
=20+9.09≈29.09
To find the mean, we use the formula:
Mean=∑(f⋅x)n
Where x is the midpoint of each class.
- For class 0-10: x=5
- For class 10-20: x=15
- For class 20-30: x=25
- For class 30-40: x=35
- For class 40-50: x=45
- 8⋅5=40
- 16⋅15=240
- 36⋅25=900
- 34⋅35=1190
- 6⋅45=270
∑(f⋅x)=40+240+900+1190+270=2640
Mean=2640100=26.4
- Mean: 26.4
- Median: 27.22
- Mode: 29.09
Topper's Solved these Questions
- MODEL QUESTION PAPER - 1 BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER - 1 EXERCISE - SECTION - B
6 Videos
- MID TERM TEST PAPER BOOK - VK GLOBAL PUBLICATIONCHAPTER - MID TERM TEST PAPER EXERCISE - SECTION -D
7 Videos
- MODEL QUESTION PAPER - 9 [UNSOLVED]BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER - 9 [UNSOLVED]EXERCISE - SECTION - D
7 Videos
Similar Questions
Find the median of the following data:
Class Interval0−1010−2020−3030−4040−50f68547
View SolutionCalculate standard deviation for the following data :
⎡⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢⎣ClassInterval(C.I.)Frequency(f)10−153215−202820−252025−301630−353435−401040−458⎤⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥⎦
View Solution
Knowledge Check
Find the median of the following data.
Class Intervalf 0−1012 10−2013 20−3025 30−4020 40−5010A25B23C24D26Find the mean of the following continuous distribution.
{("Class Interval",f),(" "0-10,8),(" "10-20,4),(" "20-30,6),(" "30-40,3),(" "40-50,4):}A20.8B21.4C21.8D22.2Find the approximate value of mean deviation about the mode of the following data.
{:("Class Interval",f),(" "0-10,4),(" "10-20,6),(" "20-30,3),(" "30-40,9),(" "40-50,5):}A11.5B12.5C13.5D14.5
Find the mean of the data given in the following table.
Class0−2020−4040−6060−8080−100Frequency 6 4 5 7 3
View SolutionFind the mean deviation about median for the following data
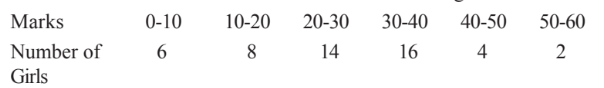
View SolutionWhat is the standard deviation of the following data ?
Measurement0−1010−2020−3030−40Frequency1342
View SolutionThe median of the following frequency distribution is
Class intervalf 0−105 10−208 20−307 30−4010 40−5020
View SolutionThe median from given grouped data would be
Class IntervalFrequencyCumulative frequency10−205520−3071230−4061840−5082650−60430
View Solution
