In the given Fig. 3, in $Δ A B C, D and E$ are the mid point of the sides AB and AC respectively. Find the length of DE. Prove that $D E = \frac{1}{2} B C .$

Video Solution

|

Answer

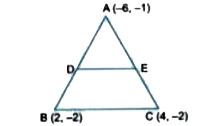
Step by step video & image solution for In the given Fig. 3, in DeltaABC, D and E are the mid point of the sides AB and AC respectively. Find the length of DE. Prove that DE = (1)/(2) BC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Area of $Δ A B C = 30 c m^{2}$ . D and E are the mid - points of BC and AB respectively. Find $A (Δ B D E)$ :
A10
B7.5
C15
Dnone of these
Question 2 - Select One
If in a triangle AB=a,AC=b and D,E are the mid-points of AB and AC respectively, then DE is equal to
A $\frac{a}{4} - \frac{b}{4}$
B $\frac{a}{2} - \frac{b}{2}$
C $\frac{b}{4} - \frac{a}{4}$
D $\frac{b}{2} - \frac{a}{2}$
Question 3 - Select One
If D, E and Fare the mid points of BC, CA and AB respectively of the ABC then the ratio of area of the parallelogram DEFB and area of the trapezlum CAFD is:
A $1 : 2$
B $2 : 3$
C $3 : 4$
D $1 : 1$

VK GLOBAL PUBLICATION-MODEL QUESTION PAPER-10 [UNSOLVED]-SECTION-C

Home
Ask Doubt
Profile