Half of the space between the plates of a parallel plate capacitor is filled with a dielectric material of dielectric constant K . The ramaining half contains air as shown in the figure . The capacitor is now given a charge Q . Then

electric field in the dielectric filled region is higher than that in the air - filled region.
on the two halves of the bottom plate the charge densities are unequal.
charge on the half of the top plate above the air filled part is QK+1.
capacitance of the capacitor shown above is (1+K)C02, where C0 is the capacitance of the same capacitor with dielectric removed.
The correct Answer is:d
Let A be area of each plate and d is the distance between the plates.
The given capacitor is equivalent to two capacitors in parallel with capacitances
C1=Kε0(A/2)d=Kε0A2d … (i)
C2=ε0(A/2)d=ε0A2d ...(ii)

∴Ceq=C1+C2=Kε0A2d+ε0A2d
=ε0A2d(K+1)=C02=(K+1), Where C0=ε0Ad
Q1Q2=C1C2=K1 ...(iii) (Using (i) and (ii))
As surface charge density , σ=ChargeArea
∴σ1σ2=Q1Q2=K1 ...(iv) (Using (iii))
Total charge , Q=Q1+Q2 ...(v)
From (iii) and (v) , we get
Q1=KQK+1andQ2=QK+1
Electric field in dielectric filled region,
E1=σ1ε0K
Electric field in air - filled region , E2=σ2ε0
∴E1E2=σ1σ2×1K=K×1K=1 (Using (iv))
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MTG-WBJEECHAPTER - ELECTROSTATICSEXERCISE - (WB JEE Previous Years Questions ) CATEGORY 2 : Single Option correct Type
8 Videos
- ELECTROMAGNETIC WAVES BOOK - MTG-WBJEECHAPTER - ELECTROMAGNETIC WAVES EXERCISE - WB JEE WORKOUT (CATEGORY 3 : ONE OR MORE THAN ONE OPTION CORRECT TYPE)
10 Videos
- GRAVITATIONBOOK - MTG-WBJEECHAPTER - GRAVITATIONEXERCISE - WB JEE Previous Years Questions (CATEGORY 1: Single Option Correct Type
7 Videos
Similar Questions
Half of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
View SolutionA paralle plate air capacitor has capacitance C. Now half of the space is fillel with a dielectric material with dielectric constant K as shown in figure . The new capacitance is C . Then

View Solution
Knowledge Check
In figure half of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
 A
A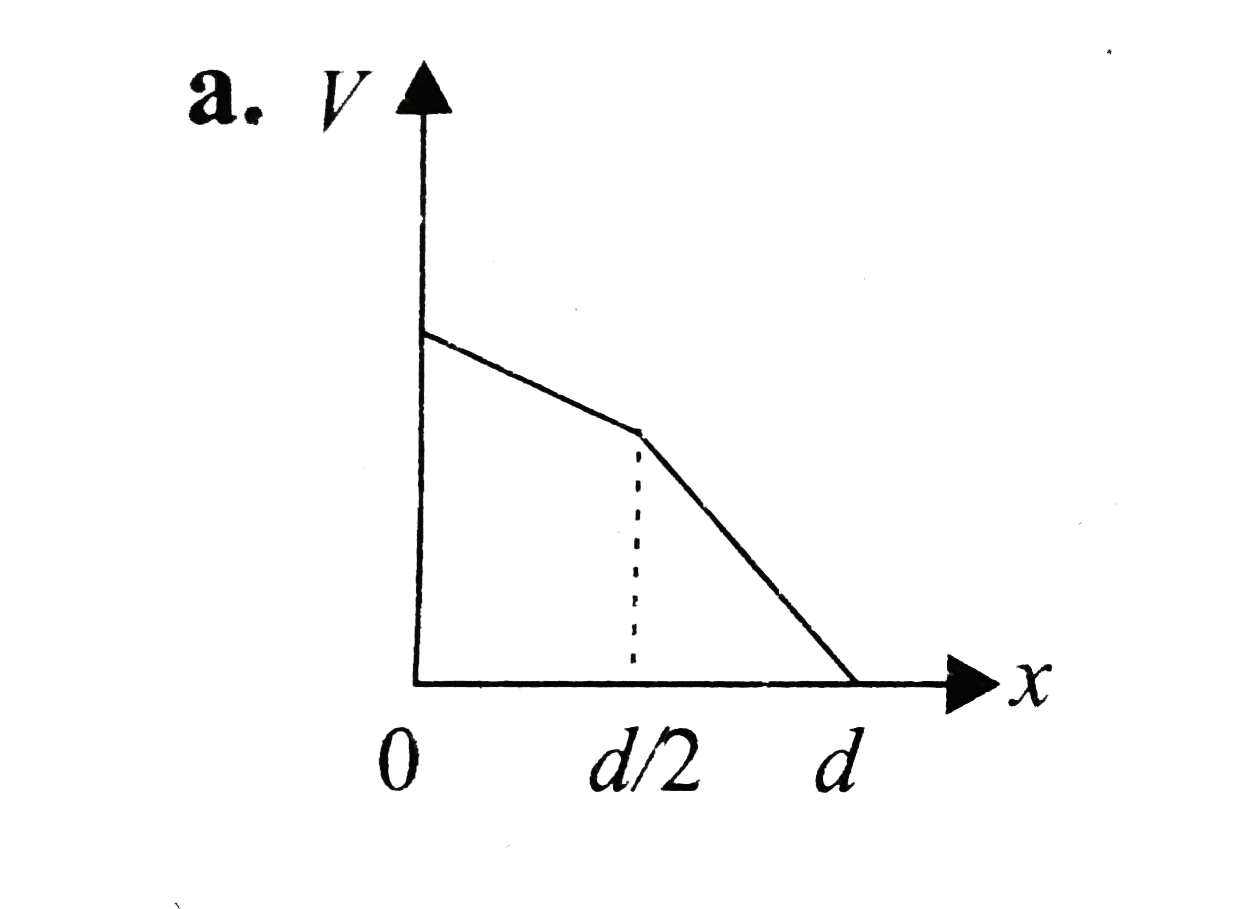 B
B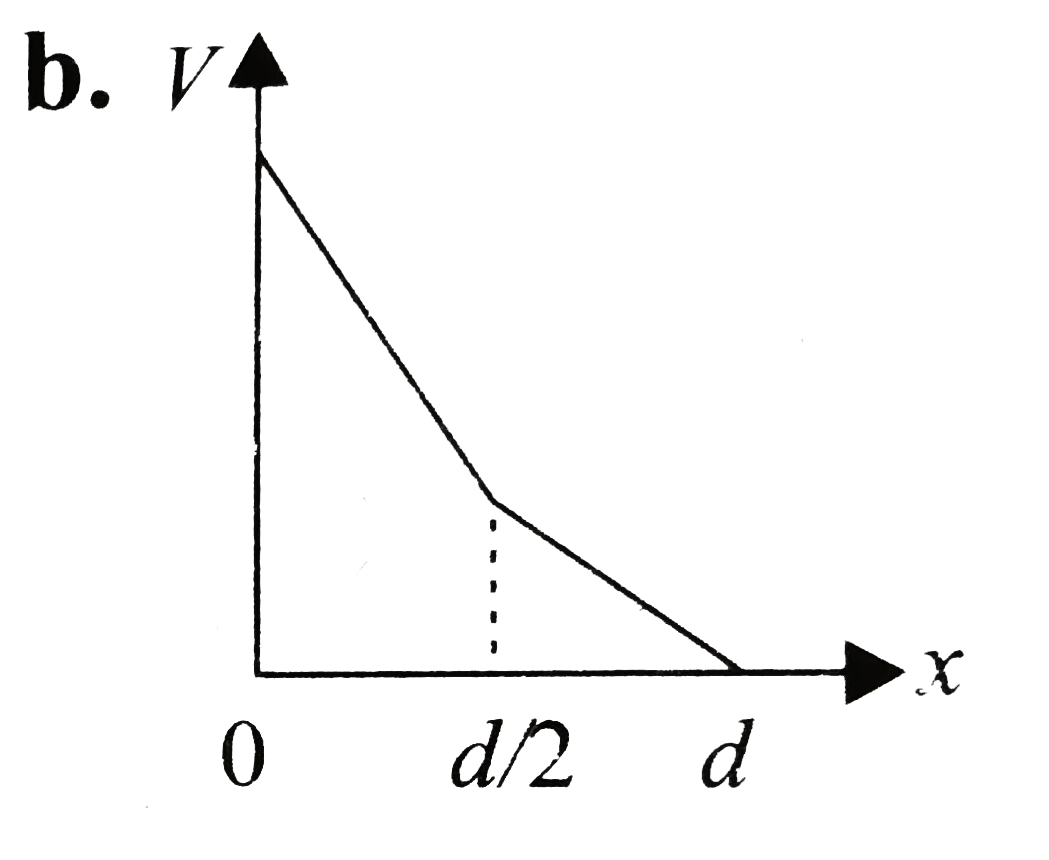 C
C D
D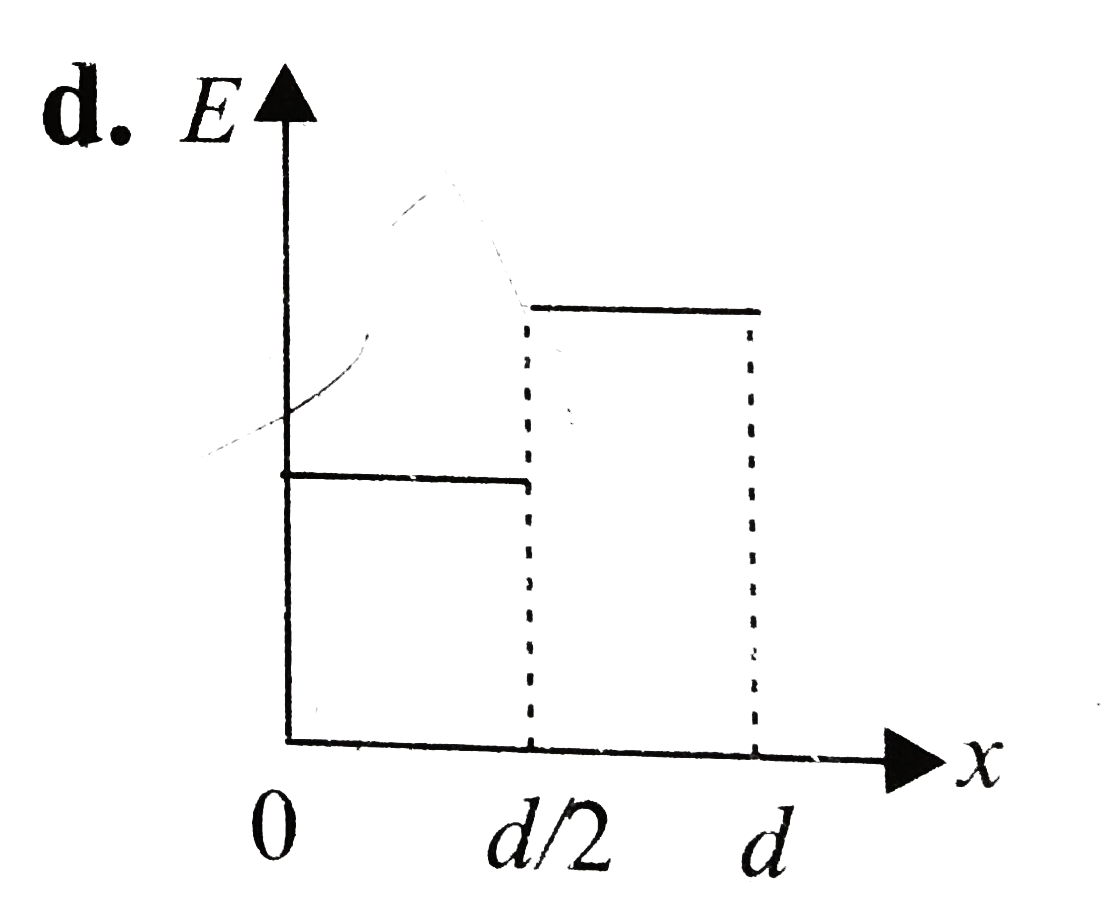
Half of the space between parallel plate capacitor is filled with a medium of dielectric constant K parallel to the plates . if initially the capacity is C, then the new capacity will be :
A2KC(1+K)BC(K+1)/2CCK/(1+K)DKCA paralle plate air capacitor has capacitance C. Now half of the space is fillel with a dielectric material with dielectric constant K as shown in figure . The new capacitance is C . Then
 AC'=C2[1+K]BC'=C[1+K]CC'=C[1+K2]DC'=C[12+K]
AC'=C2[1+K]BC'=C[1+K]CC'=C[1+K2]DC'=C[12+K]
Two parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View SolutionTwo parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View SolutionA parallel plate capacitor is charged to a certain voltage. Now if the dielectric material (with dielectric constant k ) is removed then the
View SolutionSpace between the plates of a parallel plate capacitor is filled with a dielectric slab. The capacitor is charged and then the supply is disconnected to it. If the slab is now taken out then
View SolutionA parallel plate air capacitor has a capacitance C. When it is half filled with a dielectric of dielectric constant 5, then the percentage increase in the capacitance will be

View Solution
