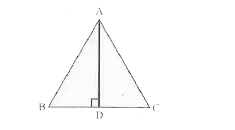
ΔABC में AD भुजा BC का लम्ब समद्धिभाजक हैं (देखिए आक्रति)| दर्शाइए कि ΔABC एक समद्धिबाहू त्रिभुज है, जिसमें AB = AC है |
The correct Answer is:ΔABD ~-= ΔACD
Topper's Solved these Questions
- BOOK - SCIENCE PUBLICATIONCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.35videos
त्रिभुज
- BOOK - SCIENCE PUBLICATIONCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.46videos
त्रिभुज
- BOOK - SCIENCE PUBLICATIONCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.17videos
त्रिभुज
- BOOK - SCIENCE PUBLICATIONCHAPTER - चतुर्भुज EXERCISE - प्रश्नावली 8.2 पर आधारित अभ्यास प्रश्न7videos
चतुर्भुज
- BOOK - SCIENCE PUBLICATIONCHAPTER - दो चरों वाले रैखिक समीकरणEXERCISE - प्रश्नावली 4.4 पर आधारित अभ्यास प्रश्न1videos
दो चरों वाले रैखिक समीकरण
Similar Questions
ΔABC और ΔDBC एक ही आधार BC पर बने दो समद्धिबाहू त्रिभुज इस प्रकार है कि A और D भुजा BC के एक ही ओर स्थित है | (देखिए आक्रति ) | यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि-
(i) ΔABD ~-= ΔACD
(ii) ΔABP ~-= ΔACP
(iii) AP कोण A और कोण D दोनों को समद्धिभाजित करता है |
(iv) AP रेखाखण्ड BC का लम्ब समद्धिभाजक है |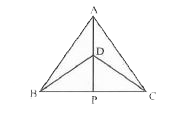
03:47View Solutionदर्शाइए क समकोण त्रिभुज में कोण सबसे लम्बी भुजा होती है |
01:37View Solutionचतुर्भुज ACBD में, AC -= AD है और AB कोण A को सम्द्धिभाजिक कहेते है (देखिए आकृति) | दर्शाइए कि ∠ABC -= ∠ABD है |
BC और BD के बारे में आप क्या कह सकते है ?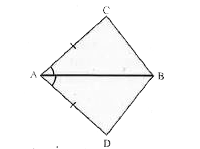
06:07View SolutionP, Q और R क्रमशः एक समबाहु त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य बिन्दु है। सिद्ध कीजिए कि ΔPQR भी एक समबाहु त्रिभुज हैं।
02:11View Solutionनिम्नलिखित समीकरणों को (i) संख्या रेखा और तथा (ii) कार्तिए तल पर प्रदर्शित कीजिए।
(a) x−2=0 " (b)2x+4=3x+1
(c) y+5=001:31View SolutionIdentify the cell organelle 'A' :-
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_BIO_C10_E08_018_Q01.png" width="80%"gt02:46View SolutionHow many lines of symmetry does the above figure have ?
02:45View SolutionWhich of the following are correct chain isomers of butane ? (i)
02:17View SolutionDetermine the point of symmetry of a regular hexagon.
05:41View SolutionDtermine the images of the following figure about the given line :
02:10View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
02:17View SolutionMatch the following Column A to Column B
02:10View SolutionMatch the following Column A to Column B
04:23View SolutionMatch the following Column A to Column B
01:13View SolutionThe inequation represented by the graph given below is :
01:19View SolutionThe inequation that best describes the graph given below is _________
03:10View Solution