A bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity vo at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for
The speeds at points B and C.
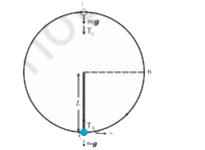
It is clear from Eq. (6.14)
vc=√gL
At B, the energy is E=12mv2B+mgL
Equatting this to the energy at A and employing the result from (i), namely v20=5gL,
12mv2B+mgL=12mv20
52mgL
vB=√3gL.
Topper's Solved these Questions
Similar Questions
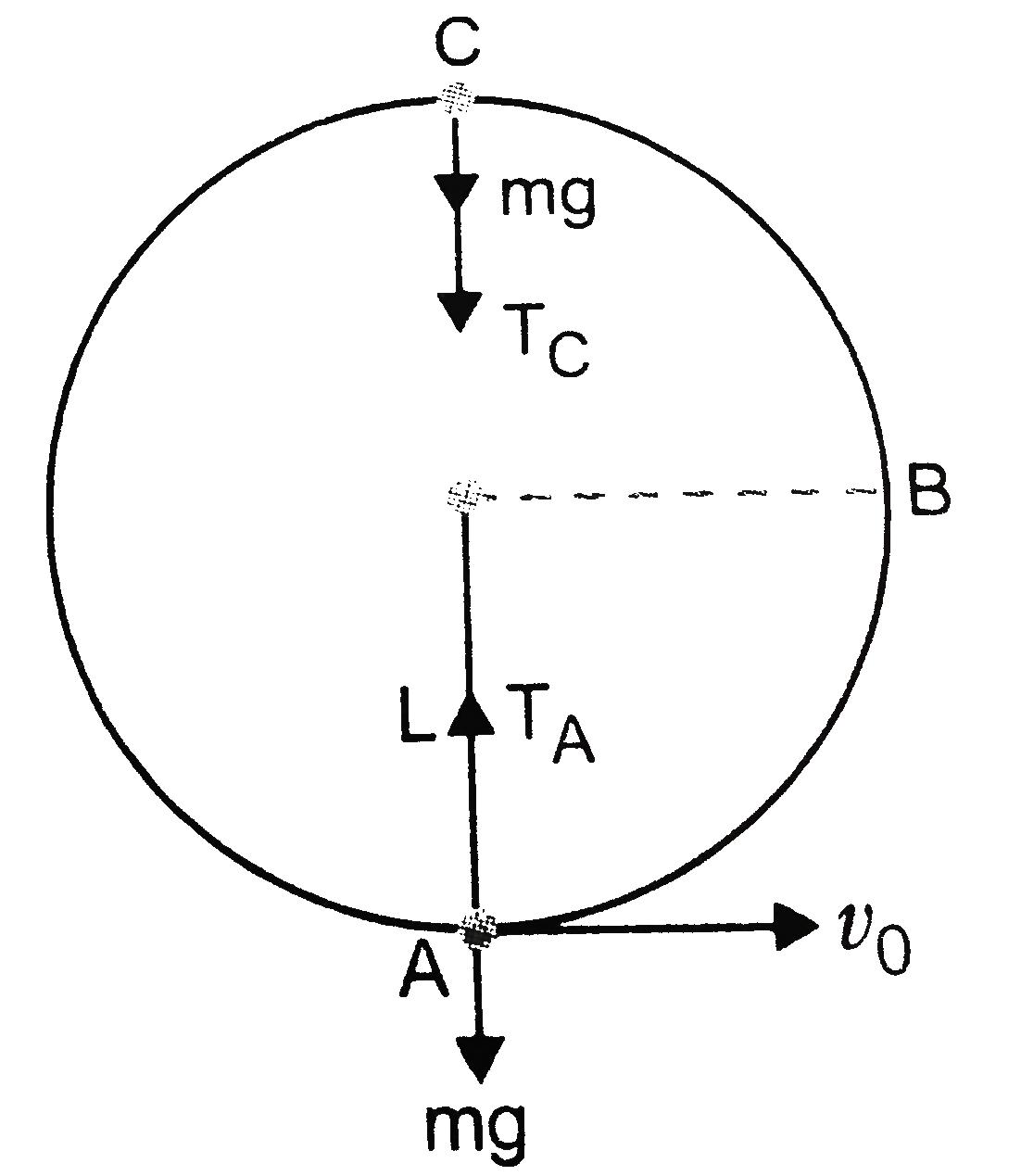
A bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v0 at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) v0 (ii) the speeds at points B and C, (ii) the ration of kinetic energies (KB/KC) at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.
 View Solution
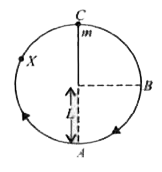
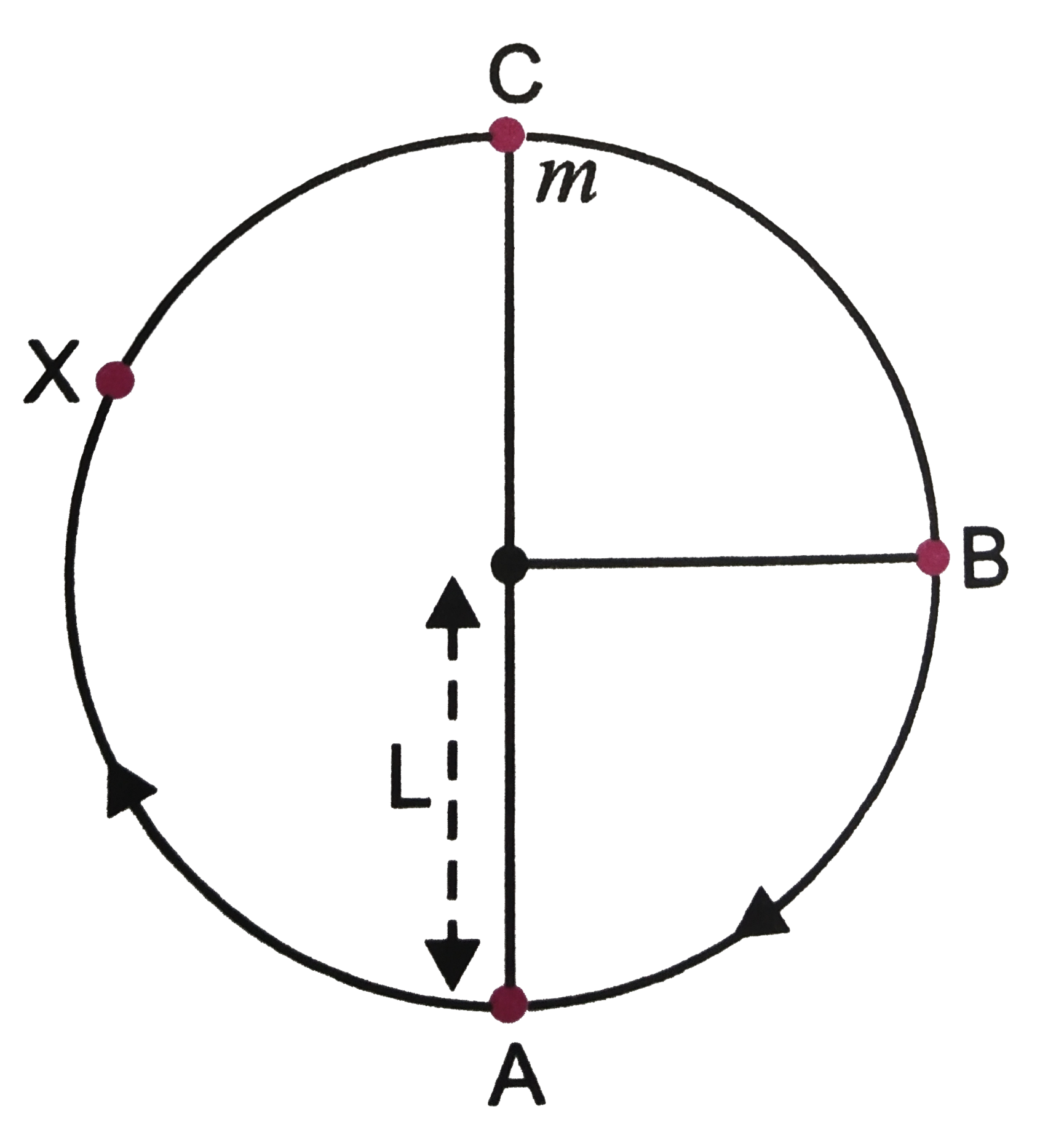
View SolutionA bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in figure. What will be X the trajectory of the particle if the string is cut at
(a) Point B
(b) Point C
(c) Point X
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v0 at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) v0 (ii) the speeds at points B and C, (ii) the ration of kinetic energies (KB/KC) at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.
 AA-p,B-q,C-s,D-rBA-q,B-r,C-q,D-sCA-r,B-s,C-q,D-pDA-s,B-p,C-r,D-q
AA-p,B-q,C-s,D-rBA-q,B-r,C-q,D-sCA-r,B-s,C-q,D-pDA-s,B-p,C-r,D-q - Question 2 - Select One
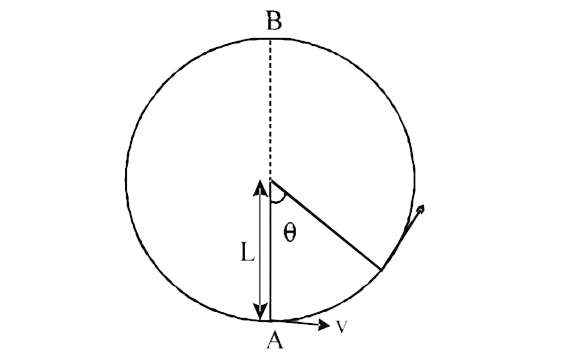
A bob of mas M is suspended by a massless string of length L. The horizontal velocity v at position A is just sufficient to make it reach the point B. The angle θ at which the speed of the bob is half of that at A, satisfies.
 .Aθ=π4Bπ4<θ<π2Cπ2<θ<3π4D3π4<θ<π
.Aθ=π4Bπ4<θ<π2Cπ2<θ<3π4D3π4<θ<π
A body is suspended by a string of length l is projected with horizontal velocity V such that it does not complete the motion in vertical circles.Then the height at which tension becomes is zero is given by?
View SolutionA bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in figure . What will be the trajectory of the particle if the string is cut at
(a) Point B ? (b) Point C? (c) Point X?
 View Solution
View SolutionA bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in figure . What will be the trajectory of the particle if the string is cut at
(a) Point B ? (b) Point C? (c) Point X?
 View Solution
View SolutionA bob of mass M is suspended by a massless string of length L. The horizontal velocity v at position A is just sufficient to make it reach the point B. The angle θ at which the speed of the bob is half of that at A, satisfies
 View Solution
View SolutionA particle in projected with velocity √3gL at point A (lowest point of the circle) in the vertical plane. Find the maximum height about horizontal level of point A if the string slacks at the point B as shown in figure.
 View Solution
View SolutionA particle in projected with velocity √3gL at point A (lowest point of the circle) in the vertical plane. Find the maximum height about horizontal level of point A if the string slacks at the point B as shown in figure.
 View Solution
View Solution

