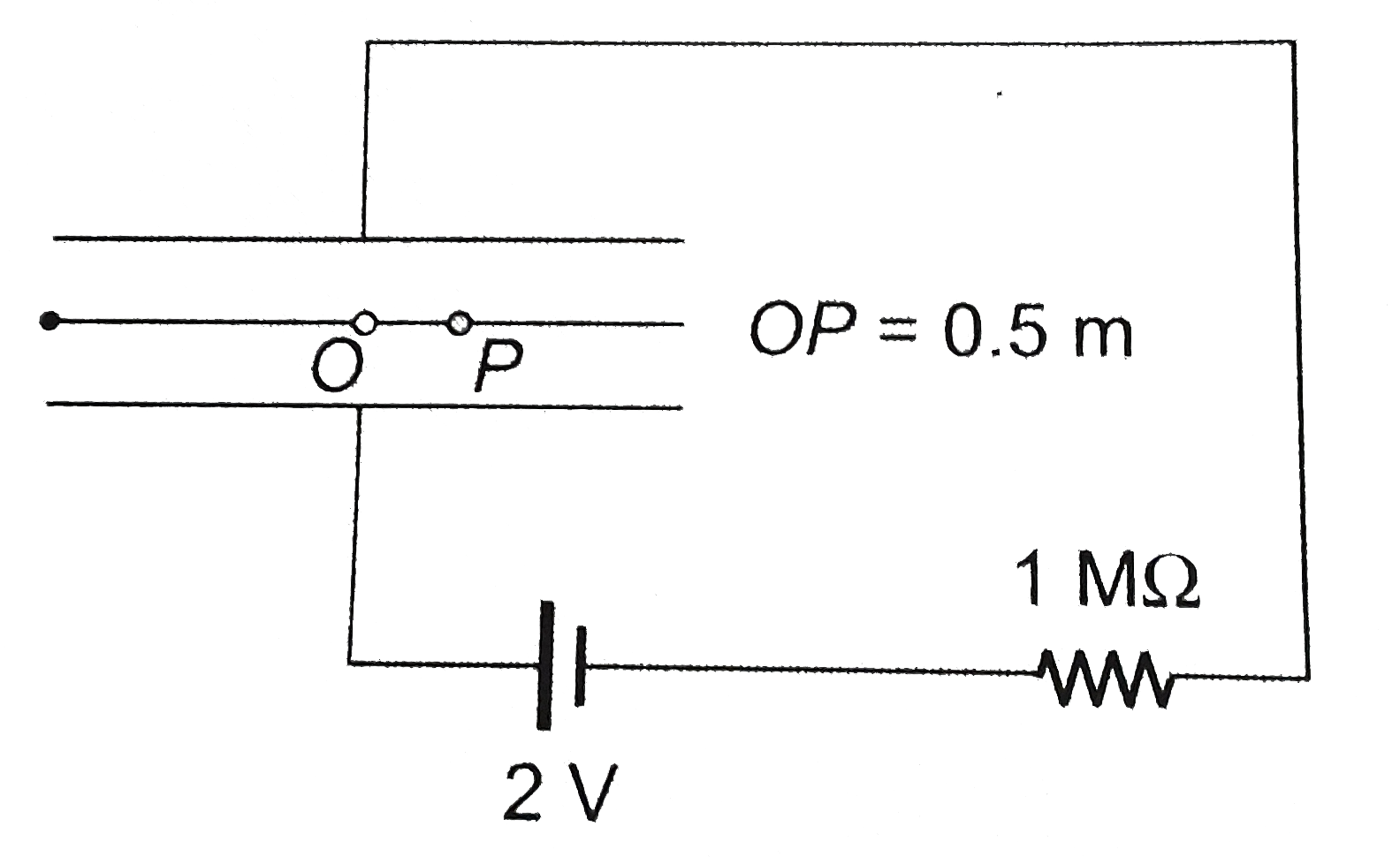
A parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor $R = 1 M Ω$ across a 2V battery (Fig. 8.3). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after $t = 10^{- 3} s$ . (The charge on the capacitor at time t is q (t) = CV [1 – exp $(- t / τ)$ ], where the time constant $τ$ is equal to CR.)

Text Solution

Verified by Experts

The time constant of the CR circuit is $τ = C R = 10^{- 3} s$ . Then, we have
$q (t) = C V [1 - exp (- t / τ)]$
$= 2 \times 10^{- 9} [1 - exp (- t / 10^{- 3})]$
The electric field in between the plates at time t is
$E = \frac{q (t)}{ε_{0} A} = \frac{q}{π ε_{0}}, A = π {(1)}^{2} m^{2}$ = area of the plates.
Consider now a circular loop of radius (1/2) m parallel to the plates passing through P. The magnetic field B at all points on the loop is along the loop and of the same value. The flux $Φ_{E}$ through this loop is
$Φ_{E} = E \times$ area of the loop
$= E \times π \times {(\frac{1}{2})}^{2} = \frac{π E}{4} = \frac{q}{4 ε_{0}}$
The displacement current
$i_{d} = ε_{0} \frac{d Φ_{E}}{d t} = \frac{1}{4} \frac{d q}{d t} = 0.5 \times 10^{- 6} exp (- 1)$
at $t = 10^{- 3} s$ . Now, applying Ampere-Maxwell law to the loop, we get
$B \times 2 π \times (\frac{1}{2}) = μ_{0} (i_{c} + i_{d}) = μ_{0} (0 + i_{d}) = 0.5 \times 10^{- 6} μ_{0} exp (- 1)$
or, $B = 0.74 \times 10^{- 13} T$

Updated on:21/07/2023

Find the charge on parallel plate capacitor having circular plates of radius 8 cm and plate separation 1 mm. The potential difference is 100 V:
A $1.78 \times 10^{- 5}$ C
B $2 \times 10^{- 9} C$
C $1.78 \times 10^{- 8}$ C
D $4.3 \times 10^{4}$ C
A parallel plate capacitor has an electric field of $10^{5} V / m$ between the plates. If the charge on the capacitor plate is $1 μ C$ , then force on each capacitor plate is-
A $0.1 N$
B $0.05 N$
C $0.02 N$
D $0.01 N$
A parallel plate capacitor has an electric field of $10^{5} V / m$ between the plates. If the charge on the capacitor plate is $1 μ C$ , the force on each capacitor plate is
A0.5 N
B0.05 N
C0.005 N
D5 N