Question

A motorboay is racing towards north at 25 km/h and the water current in that region is 10km/h in the direction of ${60}^{\circ }$ east of south . Find the resultant velocity of the boat.

Explanation

The vector `v_(b)` representing the velocity of the motorboat and the vector `v_(e)` representing the water current are shown in Fig . 4.11 in direstions specified by the problem . Using the parallelogram method of addition , the resultant R is obtained in the direction shown in the figure .

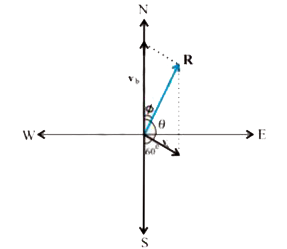
We can obtain the magnitude of R using the Law of cosine :
`R=sqrt(v_(b)^(2)+v_(c)^(2)+2v_(b)v_(c)cos120^(@))`
`=sqrt(25^(2)+10^(2)+2xx25xx10(-1//2))~=22km//h`
To obtain the direction , we apply the Law of sines
`(R)/(sintheta)=(v_(c))/(sinphi)or,sinphi=(v_(c))/(R)sintheta`
`=(10xxsin120^(@))/(21.8)=(10sqrt(3))/(2xx21.8)~=0.397`
`phi~=23.4^(@)`