There are five students S1,S2,S3,S4 and R5 arranged in a row, where initially the seat R1is allotted to the students are randomly allotted the five seats R1,R2,R3,R4 and R6 arranged in a row, where initially the seat Ri is allotted to the student Sii,=1,2,3,4,5.But,ontheexaminationday,thefivestudentsarerandomlyalloedthefiveseats.<br>(TherearetwoquestionsbasedonParagraph,thequestiongivenbelowiso≠ofthem)<br>Fori=1,2,3,4.≤tT_(i)de¬etheeventtˆthestudentsS_(1)andS_(i+1)doNOTsitadjacent→eachotheronthedayoftheexamination.Then,theprobabilityoftheeventT_(1) cap T_(2) cap T_(3) cap T_(4) is
115
110
760
16
The correct Answer is:C
Here , n(T1∩T2∩T3∩T4)
Total =−n(¯¯¯¯T1∪¯¯¯¯T2∪¯¯¯¯T3∪¯¯¯¯T4)
⇒n(T1∩T2∩T3∩T4)
=5!−[4C14!2!−(3C13!2!+3C13!2!2!)+(2C12!2!+4C12⋅2!)−2]
⇒n(T1∩T2∩T3∩T4)
=120−[192−(36+72)+(8+16)−2]
=120−[192−108+24−2]=14
∴ Required probability =14120=760
Topper's Solved these Questions
- PROBABILITYBOOK - IIT JEE PREVIOUS YEARCHAPTER - PROBABILITYEXERCISE - TOPIC 3 INDEPENDENT AND CONDITIONAL PROBABILITY OBJECTIVE QUESTION I (ONLY ONE CORRECT OPTION)
20 Videos
- PROBABILITYBOOK - IIT JEE PREVIOUS YEARCHAPTER - PROBABILITYEXERCISE - TOPIC 3 INDEPENDENT AND CONDITIONAL PROBABILITY OBJECTIVE QUESTION II (ONLY ONE CORRECT OPTION)
8 Videos
- PROBABILITYBOOK - IIT JEE PREVIOUS YEARCHAPTER - PROBABILITYEXERCISE - TOPIC 2 ADDITION AND SUBTRACTION LAW OF PROBABILITY OBJECTIVE QUESTION II (ANALYTICAL AND DESCRIPTIVE QUESTIONS )
3 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - IIT JEE PREVIOUS YEARCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Dearrangement and Number of Divisors (Fill in the Blank )
1 Videos
- RELATIONS AND FUNCTIONS BOOK - IIT JEE PREVIOUS YEARCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - All Questions
1 Videos
Similar Questions
Assume that each born child is equally likely to be a boy or a girl. If two families have two children each, then the conditional probability that all children are girls given that at least two are girls , is
View SolutionLet XandY be two events that P(X)=13,P(X|Y)=12andP(Y|X)=25 then: P(Y)=415 (b) P(X∪Y)=25 P(X′|Y)=12 (d) P(X∩Y)=15
View SolutionIn a certain city only two newspapers A and B are published, it is known that 25% of the city population reads A and 20% reads B, while 8% reads both A and B. It is also known that 30% of those who read A but not B look int advertisements and 40% of those who read B bu not A look into advertisements while 50% of those who read both A and B look into advertisements What is the percentage of the population reads an advertisement? [1984]
View SolutionThere are four balls of different colors and four boxes of colors same as those of the balls. Find the number of ways in which the balls, one in each box, could be placed in such a way that a ball does not go to box of its own color.
View Solution2sin2x+3sinx−2>0andx2−x−2<0. Find the solution set.
View SolutionThere are five students S1, S2, S3, S4 and S5 in a music class and for them there are five seats R1, R2, R3, R4 and R5 arranged in a row, where initially the seat Ri is allotted to the student Si, i=1, 2, 3, 4, 5 . But, on the examination day, the five students are randomly allotted five seats. The probability that, on the examination day, the student S1 gets the previously allotted seat R1 , and NONE of the remaining students gets the seat previously allotted to him/her is 340 (b) 18 (c) 740 (d) 15
View SolutionPARAGRAPH A There are five students S1, S2, S3, S4 and S5 in a music class and for them there are five seats R1, R2, R3, R4 and R5 arranged in a row, where initially the seat Ri is allotted to the student Si, i=1, 2, 3, 4, 5 . But, on the examination day, the five students are randomly allotted five seats. For i=1, 2, 3, 4, let Ti denote the event that the students Si and Si+1 do NOT sit adjacent to each other on the day of the examination. Then, the probability of the event T1∩T2∩T3∩T4 is 115 (b) 110 (c) 760 (d) 15
View SolutionA sphere S_(1) of radius r_(1) encloses a total charge Q. If there is another concentric sphere S_(2) of radius r_(2) (gt r_(1)) and there be no additional charges between S_(1) and S_(2) find the ration of electric flux through S_(1) and S_(2) ,
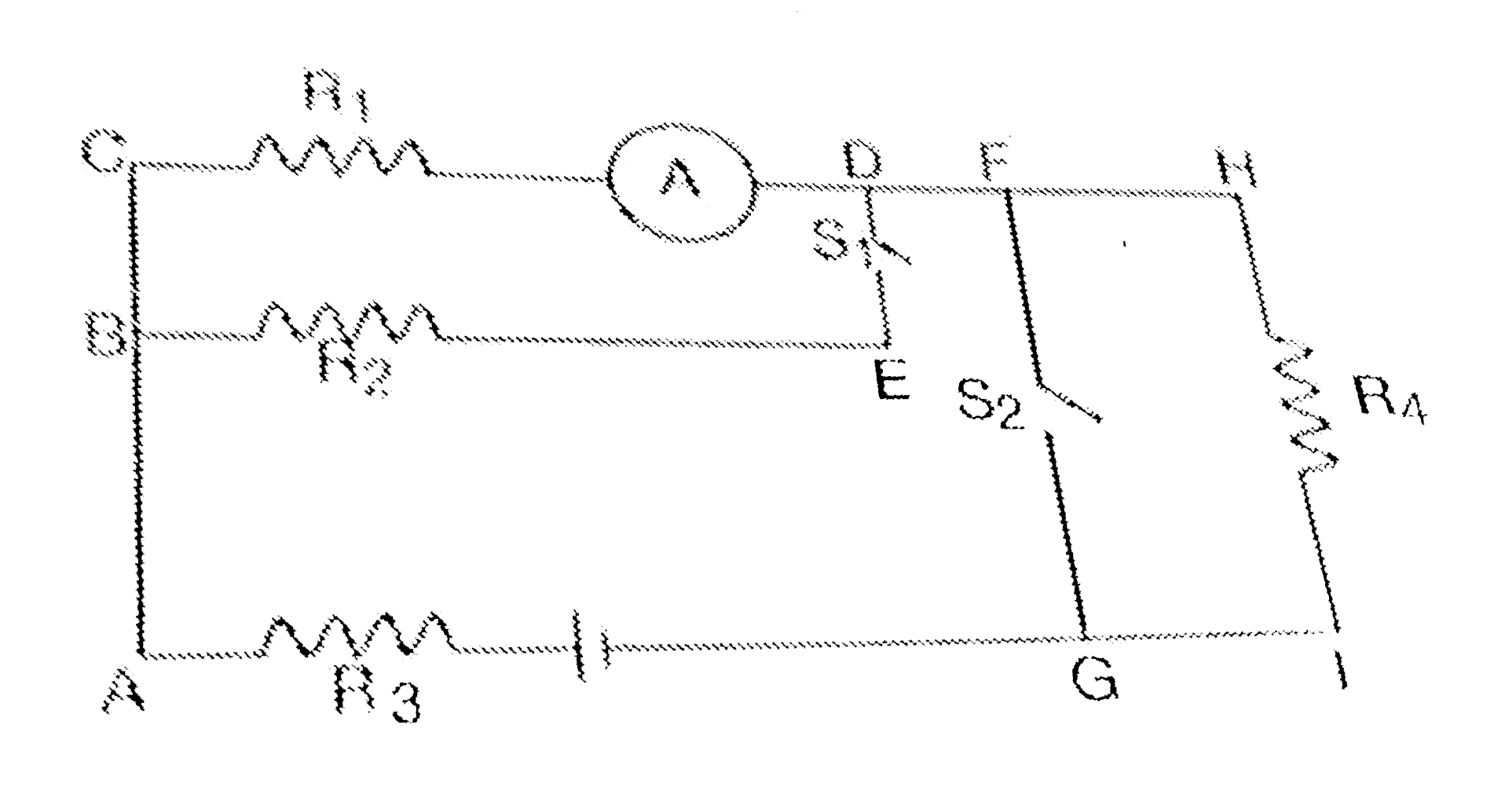
View SolutionThe resistors R1,R2,R3 and R4 are connected as shown in the figure. S1 and S2 are two switches . Discuss the flow of current through the resistors when
(1) S1 and S2 both are closed.
(2) S1 and S2 both are open.
(3) S1 is closed and S2 in open.
View SolutionThere are five students S1,S2,S3,S4 and R5 arranged in a row, where initially the seat R1is allotted to the students are randomly allotted the five seats R1,R2,R3,R4 and R6 arranged in a row, where initially the seat Ri is allotted to the student Sii,=1,2,3,4,5.But,ontheexaminationday,thefivestudentsarerandomlyalloedthefiveseats.<br>(TherearetwoquestionsbasedonParagraph,thequestiongivenbelowiso≠ofthem)<br>Theprobabilitytˆ,ontheexaminationday,thestudentS_(1)≥tsthepreviouslyalloedseatR_(1), and NONE of the remaining students gets the seat previously allotted to him/her is
View Solutionएक संगीत की कक्षा में पाँच छात्र S1,S2,S3,S4 और S5 है और उनके लिए बैठने के पाँच स्थान R1,R2,R3,R4 और R5 एक पंक्ति में व्यवस्थित हैं, जहाँ शुरूआत में स्थान Ri छात्र Si,i=1,2,3,4,5 को आवंटित किया जाता है। लेकिन परीक्षा के दिन पाँचों छात्रों को पाँच स्थान यादृच्छिक आवंटित किये जाते है
परीक्षा के दिन छात्र S1 को उसका पूर्व आवंटित स्थान R1 मिलने तथा शेष छात्रों में से किसी को भी उसका पूर्व आवंटित स्थान नहीं मिलने की प्रायिकता है
View Solutionएक संगीत की कक्षा में पाँच छात्र S1,S2,S3,S4 और S5 है और उनके लिए बैठने के पाँच स्थान R1,R2,R3,R4 और R5 एक पंक्ति में व्यवस्थित हैं, जहाँ शुरूआत में स्थान Ri छात्र Si,i=1,2,3,4,5 को आवंटित किया जाता है। लेकिन परीक्षा के दिन पाँचों छात्रों को पाँच स्थान यादृच्छिक आवंटित किये जाते है
माना कि Ti(i=1,2,3,4) उस घटना को दर्शाता है कि परीक्षा के दिन छात्र Si और Si+1 एक दूसरे के साथ - साथ नहीं बैठते हैं। तब, घटना T1∩T2∩T3∩T4 की प्रायिकता है
View SolutionA sphere S1 of radius r1 encloses a total charge Q. If there is another concentric sphere S2 of radius r2(>r1) and there be no additional charges between S1andS2 find the ratio of electric flux through S1andS2,
View SolutionPARAGRAPH A There are five students S1, S2, S3, S4 and S5 in a music class and for them there are five seats R1, R2, R3, R4 and R5 arranged in a row, where initially the seat Ri is allotted to the student Si, i=1, 2, 3, 4, 5 . But, on the examination day, the five students are randomly allotted five seats. For i=1, 2, 3, 4, let Ti denote the event that the students Si and Si+1 do NOT sit adjacent to each other on the day of the examination. Then, the probability of the event T1∩T2∩T3∩T4 is 115 (b) 110 (c) 760 (d) 15
View Solutionएक संगीत की कक्षा में पाँच छात्र S1,S2,S3,S4 और S5 है और उनके लिए बैठने के पाँच स्थान R1,R2,R3,R4 और R5 एक पंक्ति में व्यवस्थित हैं, जहाँ शुरूआत में स्थान Ri छात्र Si,i=1,2,3,4,5 को आवंटित किया जाता है। लेकिन परीक्षा के दिन पाँचों छात्रों को पाँच स्थान यादृच्छिक आवंटित किये जाते है
परीक्षा के दिन छात्र S1 को उसका पूर्व आवंटित स्थान R1 मिलने तथा शेष छात्रों में से किसी को भी उसका पूर्व आवंटित स्थान नहीं मिलने की प्रायिकता है
View Solution
