A circle passes through three points A, B and C with the line segment AC as its diameter. A line passing through A intersects the chord BC at a point D inside the circle.If angles DAB and CAB are α and β respectively and the distance between the point A and the mid-point of the line segment DC is d, prove that the area of the circle is πd2cos2acos2α+cos2β+2cosαcosβcos(β−α)
Let the radius of the circle be r. Take X - axis along AC and the O(0,0) as centre of the circle . Therefore, coordinate of A and C are (−r,0)and(r,0), respectively.
Now, ∠BAC=β,∠BOC=2β
Therefore, coordinates of B are (rcos2β,rsin2β).
Any slope of AD is tan(β−α) .
Let (x,y) be the coordinates of the point D. Equation of AD is

y=tan(β−α)(x+r) ... (i)
[∵ slope = tan(β−α) and points is (−r,0)]
Now, equation of BC is
y=rsin2β−0rcos2β−r(x−r)
⇒ y=r⋅2sinβcosβr(−2sin2β)(x−r)
⇒ y=2sinβcosbeta−2sin2β(x−r)
⇒ y=−cotβ(x−r) ...(ii)
To obtain the coordinates of D, solve Eqs. (i) and (ii) simultaneously
⇒ tan(β−α)(x+r)=−cotβ(x−r)
⇒xtan(β−α)+rtan(β−α)=−xcotβ+rcosβ
⇒x[tan(β−α)+cotβ]=r[cotβ−tan(β−α)]
⇒x[sin(β−α)cos(β−α)+cosβsinβ]=r[cosβsinβ−sin(β−α)cos(β−α)]
⇒x[sin(β−α)sinβ+cos(β−α)cosβcos(β−α)sinβ]
=r[cosβcos(β−α)−sinβsin(β−α)sinβcos(β−α)]
⇒x[cos(β−α−β)]=r[cos(β−α+β)]
⇒ x=rcos(2β−α)cosα
On putting this value in Eq. (ii), we get
y=−cosβ[rcos(2β−α)cosα−r]
⇒y=−cosβ⋅rsinβ[cos(2β−α)−cosαcosα]
⇒y=−rcosβsinβ⎡⎢
⎢⎣2sin(2β−α+α2)sin(α−2β+α2)cosα⎤⎥
⎥⎦
⇒y=−rcosβsinβ[2sinβ⋅sin(α−β)cosα]
=−2rcosβsin(α−β)/cosα
Therefore, coordinates of D are
(rcos(2β−α)cosα,−2rcosβsin(α−β)cosα)
Thus, coordinates of E are
(rcos(2β−α)+rcosα2cosα,−rcosβsin(α−β)cosα)
⇒r2cos(2β−α+α2)⋅cos(2β−α−α2)2cosα,rcosβsin(β−α)cosα
⇒rcosβ⋅cos(β−α)cosα,rcosβsin(β−α)cosα
Since, AE = d, we get
d2=r2[cosβcos(β−α)cosα+1]2+r2[cosβsin(β−α)cosα]2
=r2cos2α[cos2βcos2(β−α)+cos2α+2cosβcos(β−α)cosα+cos2βsin2(β−α)]
=r2cos2α[cos2β+cos2α+2cosαcosβcos(β−α)]
⇒r2=d2cos2αcos2β+cos2α+2cosαcosβcos(β−α)
Therefore, area of the circle.
πr2=πd2cos2αcos2β+cos2α+2cosαcosβcos(β−α)
Topper's Solved these Questions
- CIRCLEBOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 1 Integer Answer Type Questions
2 Videos
- CIRCLEBOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 1 Paragraph Based Questions
2 Videos
- CIRCLEBOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 1True/False
1 Videos
- BINOMIAL THEOREMBOOK - IIT JEE PREVIOUS YEARCHAPTER - BINOMIAL THEOREMEXERCISE - Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )
8 Videos
- COMPLEX NUMBERSBOOK - IIT JEE PREVIOUS YEARCHAPTER - COMPLEX NUMBERSEXERCISE - TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY (INTEGER ANSWER TYPE QUESTION)
1 Videos
Similar Questions
Knowledge Check
A circle passes through the point (-1,7) and touches the line y = x at (1, 1). Its diameter is
A4√2B5C5√2D6A line segment passing through the centre of a circle and whose end points lie on the circle is called
AdiameterBradiusCsectorDnone of these
If a number of circles pass through the end points P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.
View Solution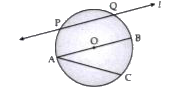
Take two points A and C on the circle, them the line segment joining the point A and C is called a ………... of the circle.
View SolutionFind the slope of the line which passes through the origin and the mid-point of the line segment joining the points A(0,−4)andB(8,0).
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View SolutionFind the equation of a line perpendicular to the line xa+yb−1 and passes through the mid-point of the line segment lying between the axes of the given line.
View SolutionA circle passes through the points of intersection of the line x=0 and the circle x2+y2+2x=3. If this circle passes through (√3,0) then its centre is :
View Solution

