Two parallel chords of a circle of radius 2 are at a distance √3+1 apart. If the chord subtend angles πkand2πk at the center, where k>0, then the value of [k] is _____
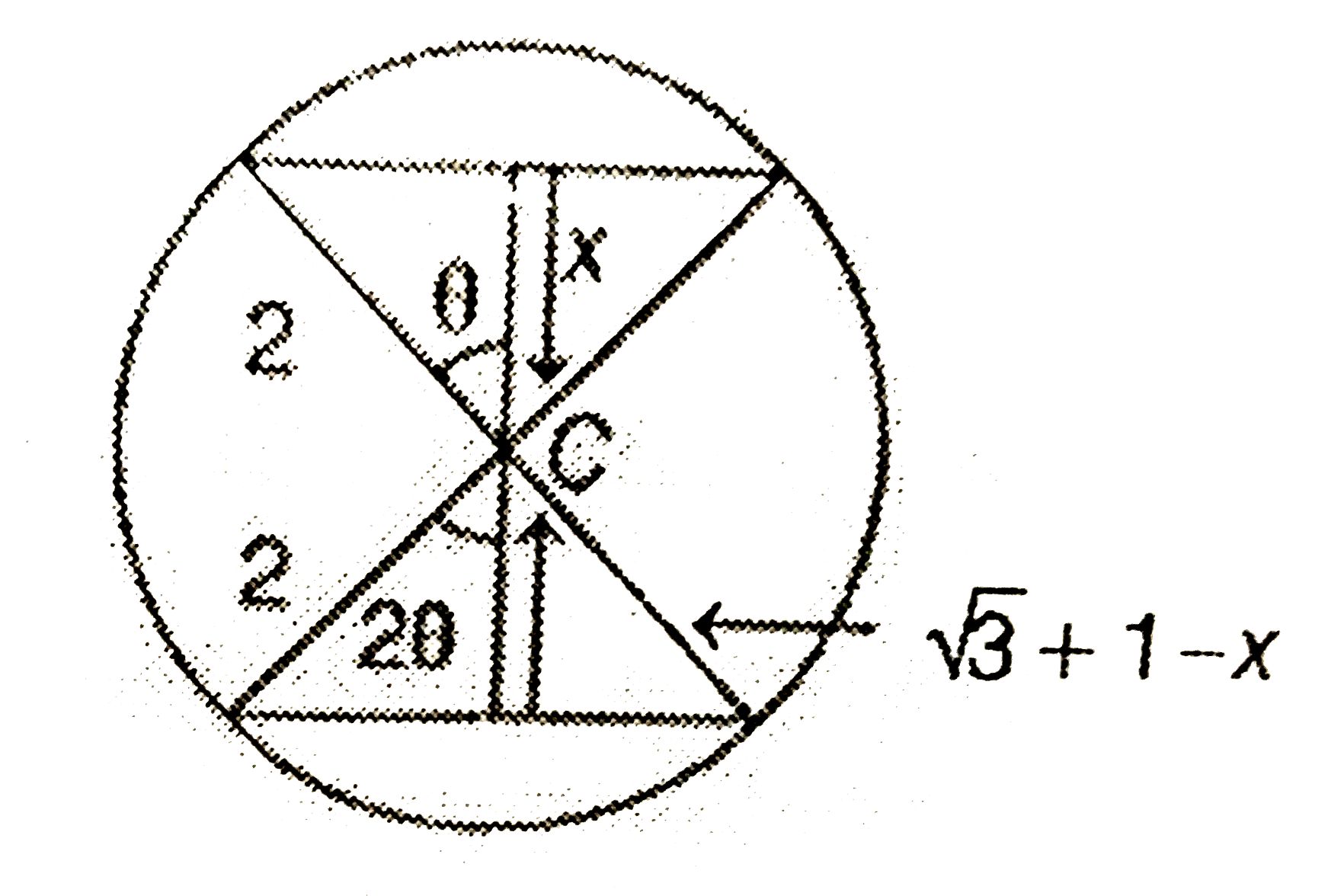 1
1
Let θ=π2k⇒cosθ=x2
⇒cos2θ=√3+1−x2
⇒2cos2θ−1=√3+1−x2
⇒2(x24)−1=√3+1−x2
⇒x2+x−3−√3=0
⇒x=−1±√1+12+4√32
=−1±√1+12+4√32=−1+2√3+12=√3
∴cosθ=√32⇒θ=π6
∴ Required angle =πk=2θ=π3
⇒k=3
Topper's Solved these Questions
- CIRCLEBOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 5 Analytical & Descriptive Questions
8 Videos
- BINOMIAL THEOREMBOOK - IIT JEE PREVIOUS YEARCHAPTER - BINOMIAL THEOREMEXERCISE - Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )
8 Videos
- COMPLEX NUMBERSBOOK - IIT JEE PREVIOUS YEARCHAPTER - COMPLEX NUMBERSEXERCISE - TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY (INTEGER ANSWER TYPE QUESTION)
1 Video
Similar Questions
Two parallel chords of a circle of radius 2 are at a distance √3+1 apart. If the chord subtend angles πkandπ2k at the center, where k>0, then the value of [k] is _____
View SolutionTwo parallel chords of a circle of radius 2 are at a distance. √3+1 apart. If the chord subtend angles πk and 2πk at the center, where k>0, then the value of [k] is
View SolutionTwo parallel chords of a circle of radius 2 are at a distance √3+1 apart. If the chord subtend angles πkand2πk at the center, where k>0, then the value of [k] is _____
View SolutionTwo parallel chords of a circle of radius 2 are at a distance √3+1 apart. If the chords subtend at the centre, angle of πk and 2πk where k>0. Then the value of [k] is
View SolutionTwo parallel chords of a circle of radius 2 are at a distance √3+1 apart. If the chords subtend at the centre, Angles of πk and 2πk, where k > 0 then the value of [k] is :
View SolutionTwo parallel chords of a circle of radius 2 are at a distance √3+1 apart. If the chords subtend at the centre, Angles of πk and 2πk, where k > 0 then the value of [k] is :
View SolutionTwo parallel chords of a circle of radius 2 units are (√3+1) units apart. If these chords subtend, at the centre, angles of 90∘k and 180∘k, where kgt0, then find the value of k.
View SolutionLet PQ and RS be two parallel chords of a given circle of radius 6 cm, lying on the same side of the center. If the chords subtends angles of 72∘and 144∘ at the center and the distance between the chords is d, then d2 is equal to
View SolutionIf ∫π0(|cosx|)3dx=k+1k, where k>0, then the value of k is:
View SolutionAB and CD are two parallel chords of a circle of radius 6 cm lying on the same side of the centre. If the chords subtend angles of 72∘ and 144∘ at the centre, find the distance between the chords.
View Solution