Let the curve C be the mirror image of the parabola $y^{2} = 4 x$ with respect to the line $x + y + 4 = 0$ . If A and B are the points of intersection of C with the line $y = - 5$ , then the distance between A and B is

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Let $P (t^{2}, 2 t)$ be a point on the curve $y^{2} = 4 x$ , whose image is Q(x,y) on x + y + 4 = 0, then
$\frac{x - t^{2}}{1} = \frac{y - 2 t}{1} = \frac{- 2 (t^{2} + 2 t + 4)}{1^{2} + 1^{2}}$
$\Rightarrow x = - 2 t - 4$
and $y = - t^{2} - 4$

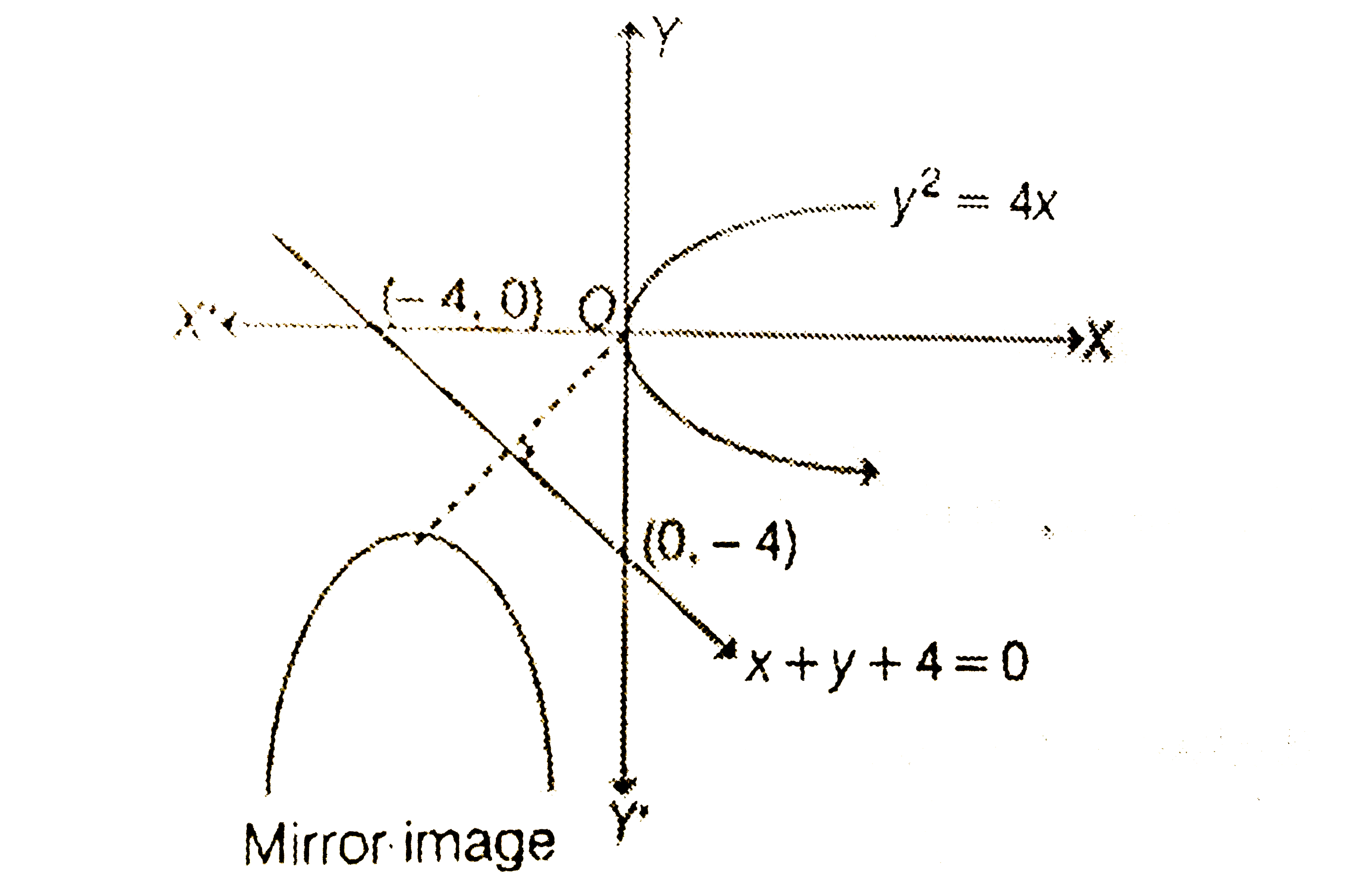
Now, the straight line y = - 5 meets the mirror image.
$∴ - t^{2} - 4 = - 5$
$\Rightarrow t^{2} = 1$
$\Rightarrow t = = \pm 1$
Thus, points of intersection of A and B are -6, - 5) and (-2,-5).
$∴$ Distance, $A B = \sqrt{{(- 2 + 6)}^{2} + {(- 5 + 5)}^{2}} = 4$

|

Updated on:21/07/2023

Class 12 MATHS PARABOLA

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The image of the parabola $y^{2} = 4 x$ about the line x-y+1=0 is
A ${(x + 1)}^{2} = 4 (y - 1)$
B ${(x - 1)}^{2} = 4 (y + 1)$
C ${(x + 1)}^{2} = - 4 (y + 1)$
D ${(x - 1)}^{2} = - 4 (y - 1)$
Question 2 - Select One
The image of the point (4,-13) with respect to the line mirror 5x+y+6=0 is
A(-1,14)
B(1,-14)
C(-1,-14)
D(1,14)
Question 3 - Select One
The angle between tangents to the parabola $y^{2} = 4 a x$ at the point where it intersects with the line $x - y - a = 0$
A $π / 3$
B $π / 4$
C $π / 6$
D $π / 2$

IIT JEE PREVIOUS YEAR-PARABOLA-TOPIC 1 EQUATION OF PARABOLA AND FOCAL CHORD (INTERGER )

Home
Ask Doubt
Profile