Let PQ be a focal chord of the parabola $y^{2} = 4 a x$ . The tangents to the parabola at P and Q meet at a point lying on the line y = 2x + a, $a > 0$ .
If chord PQ subtends an angle $θ$ at the vertex of $y^{2} = 4 a x$ , then $tan θ$ is equal to

A

$\frac{2}{3} \sqrt{7}$

B

$\frac{- 2}{3} \sqrt{7}$

C

$\frac{2}{3} \sqrt{5}$

D

$\frac{- 2}{3} \sqrt{5}$

Text Solution

Verified by Experts

The correct Answer is:D

$m_{O P} = \frac{2 a t - 0}{a t^{2} - 0} = \frac{2}{t}$

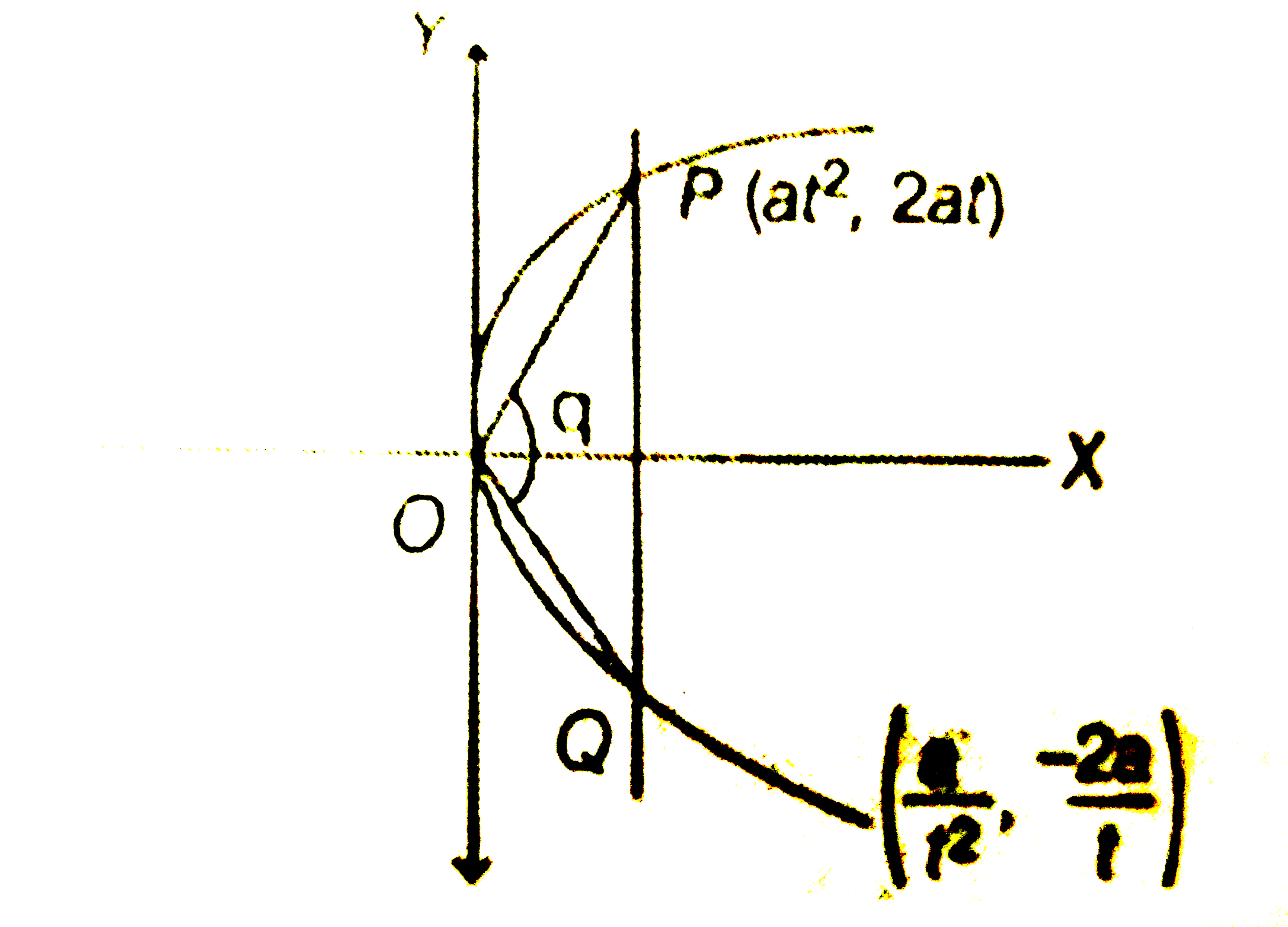
$m_{O Q} = \frac{- 2 a / t}{a / t^{2}} = - 2 t$
$∴ Tan θ = \frac{\frac{2}{t} + 2 t}{1 - \frac{2}{t} .2 t} = \frac{2 (t - \frac{1}{t})}{1 - 4} = \frac{- 2 \sqrt{5}}{3}$
Where $t + \frac{1}{} = \sqrt{5}$

Updated on:21/07/2023

|

Class 12 MATHS PARABOLA

Topper's Solved these Questions

Similar Questions

Knowledge Check

'Let PQ be a focal chord of the parabola $y^{2} = 4 a x$ . The tangents to the parabola at P and Q meet at a point lying on the line $y = 2 x + a, a > 0$ ''
Length of chord PQ is
A7a
B5a
C2a
D3a
Let PQ be a focal chord of the parabola $y^{2} = 4 a x$ . The tangents to the parabola at P and Q meet at a point lying on the line $y = 2 x + a, a > 0$ .
Length of chord PQ is:
A7a
B5a
C2a
D3a
Let PQ be a focal chord of the parabola $y^{2} = 4 a x$ . The tangents to the parabola at P and Q meet at point lying on the line
$y = 2 x + a, a < 0$ .
If chord PQ subtends an angle $θ$ at the vertex of $y^{2} = 4 a x$ , then $tan θ =$
A $2 \sqrt{7} / 3$
B $- 2 \sqrt{7} / 3$
C $2 \sqrt{5} / 3$
D $- 2 \sqrt{5} / 3$

IIT JEE PREVIOUS YEAR-PARABOLA-TOPIC 4 DIAMETER, CHORD OF CONTACT, CHORD BISECTED AND PRODUCT OF PAIR OF TANGENTS OBJECTIVES QUESTION II (PASSAGE BASED PROBLEMS )

Home
Ask Doubt
Profile