The area of rectangle is twice the area of a triangle. The p"rimeter of the rectangle is 58 cm. What is the area of the triangle ?
106cm2
108cm2
104cm2
Cannot be determined
The correct Answer is:D
To solve the problem step by step, we will use the information given about the rectangle and the triangle.
Step 1: Understand the relationship between the areas
We know that the area of the rectangle (A_rect) is twice the area of the triangle (A_tri). This can be expressed mathematically as:
Arect=2×Atri
Step 2: Use the perimeter of the rectangle
The perimeter (P) of a rectangle is given by the formula:
P=2×(L+B)
where L is the length and B is the breadth of the rectangle. We are given that the perimeter is 58 cm:
2×(L+B)=58
Step 3: Simplify the perimeter equation
Dividing both sides of the equation by 2 gives us:
L+B=29
Step 4: Express the area of the rectangle
The area of the rectangle can be expressed as:
Arect=L×B
Step 5: Substitute the area relationship
From Step 1, we know:
Arect=2×Atri
Thus, we can write:
L×B=2×Atri
Step 6: Find the area of the triangle
To find the area of the triangle, we need to express it in terms of the rectangle's area:
Atri=L×B2
Step 7: Determine the values of L and B
Since we only know that L+B=29 and we do not have specific values for L and B, we cannot determine a unique area for the triangle. The area of the triangle depends on the specific values of L and B.
Conclusion
Since we cannot determine the specific dimensions of the rectangle, we cannot find a unique area for the triangle. Therefore, the area of the triangle cannot be determined with the given information.
Final Answer
The area of the triangle cannot be determined.
---
We know that the area of the rectangle (A_rect) is twice the area of the triangle (A_tri). This can be expressed mathematically as:
Arect=2×Atri
The perimeter (P) of a rectangle is given by the formula:
P=2×(L+B)
where L is the length and B is the breadth of the rectangle. We are given that the perimeter is 58 cm:
2×(L+B)=58
Dividing both sides of the equation by 2 gives us:
L+B=29
The area of the rectangle can be expressed as:
Arect=L×B
From Step 1, we know:
Arect=2×Atri
Thus, we can write:
L×B=2×Atri
To find the area of the triangle, we need to express it in terms of the rectangle's area:
Atri=L×B2
Since we only know that L+B=29 and we do not have specific values for L and B, we cannot determine a unique area for the triangle. The area of the triangle depends on the specific values of L and B.
Since we cannot determine the specific dimensions of the rectangle, we cannot find a unique area for the triangle. Therefore, the area of the triangle cannot be determined with the given information.
The area of the triangle cannot be determined.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The area of a rectangle is 4 times the area of a square. The length of the rectangle is 90 cm and the breadth of the rectangle is 2/3rd of the side of the square. What is the side of the square?
A10 cmB20 cmC15 cmDCouldn't be determined - Question 2 - Select One
The area of a rectangle is 4 times the area of a square .The length of the rectangle is 90 cm and the breadth of the rectangle is 2/3 of the square.What is the side of the square ?
A10 cmB20 cmC9 cmDNone of these - Question 3 - Select One
Length of rectangle is twice its breadth, if perimeter of the rectangle is 78 m, then what will be the area of the rectangle?
A300m2B338m2C169m2D507m2
The difference between the length and the breadth of a rectangle is 7 Cms and the perimeter of the rectangle is 50 Cms What is the area of the rectangle ?
View SolutionThe area of a rectangle is 1.8 times the area of a square. The length of the rectangle is 5 times the breadth. The side of the square is 20 cm. What is the perimeter of the rectangle?
View SolutionThe area of a right- angled triangle is two-thirds of the area of a rectangle. The base of the triangle is 80 percent of the breadth of the reactangle. If the perimeter of the rectangle is 200 cm, what is the height of the triangle?
View SolutionThe area of a rectangle is 4 times the area of a square. The area of the square is 729 sq cm and the length of the rectangle is 81 cm. What is the difference between the side of the square and the breadth of the rectangle?
View SolutionABCD is a rectangle and there are four equilateral triangles . Area of ΔASD equals to area of ΔBQC and area of ΔDRC equals to area of ΔAPB. The perimeter of the rectangle is 12 cm. Also the sum of the areas of the four triangles is 10√3cm2 then the total area of the figures thus formed :
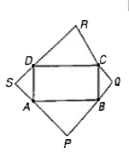 View Solution
View Solution