Four circles having equal radii are drawn with centres at the four corners of a square. Each circle touches the other two adjacent circles. If the remaining area of the square is 168 cm2, what is the size of the radius of the circle? (in centimeters) (a) 14 (b) 1.4 (c) 35 (d) 21

A

14

B

1.4

C

35

D

21

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Let the radius of each circle be 'r' cm.

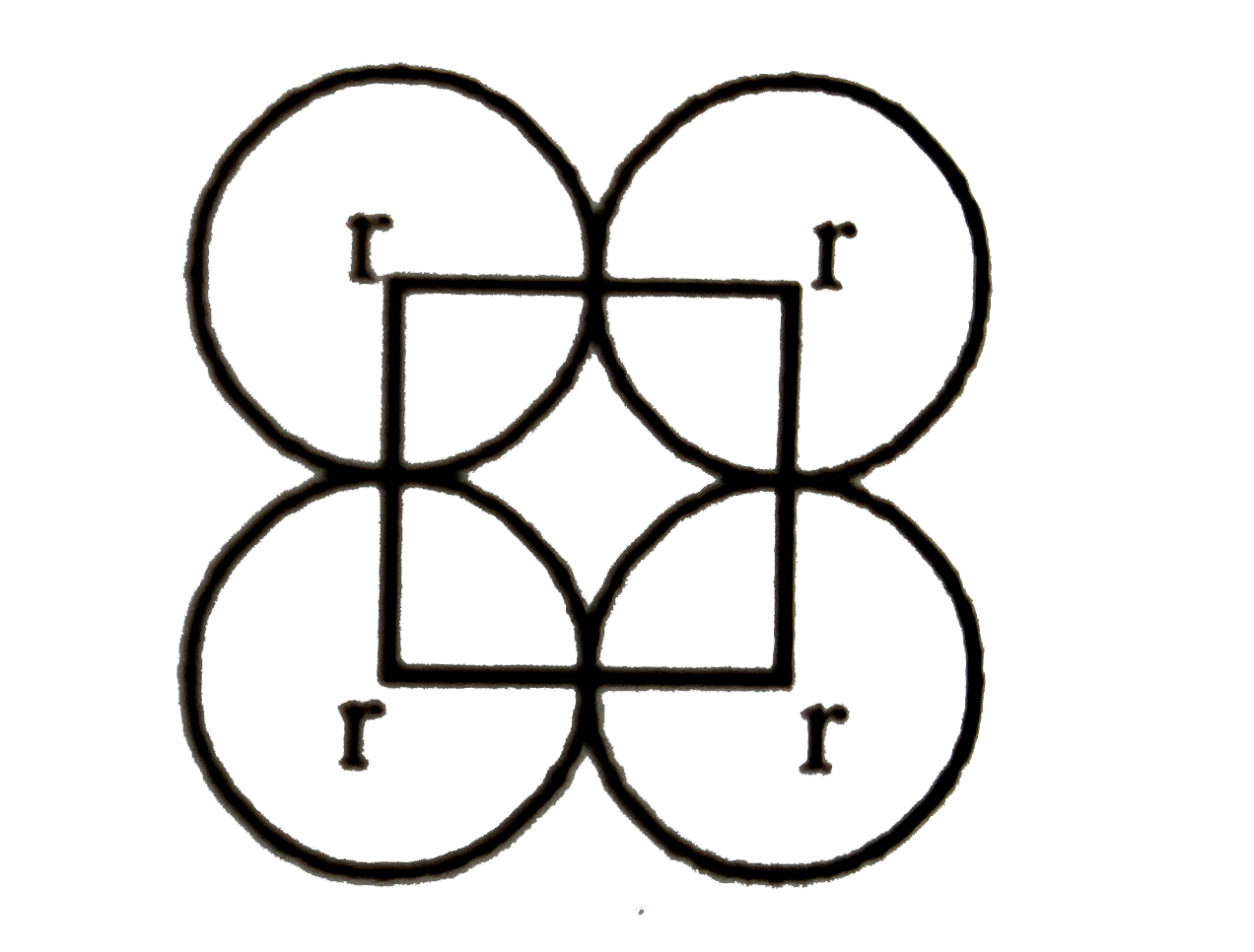
Then, the side of the square will be '2r' cm.
Area of the square $= {(2 r)}^{2} = 4 r^{2} c m^{2}$
Now, according to the question.
Remaining area of the square
$= 4 r^{2} - π r^{2}$
$∴ 4 r^{2} - π r^{2} = 168$
$or, r^{2} (4 - \frac{22}{7}) = 168$
$or, r^{2} \times (28 - 22) = 168 \times 7$
or, $r^{2} = \frac{168 \times 7}{6} = 28 \times 7 = 7 \times 4 \times 7$
$∴ r = \sqrt{7 \times 7 \times 4} = 7 \times 2 = 14 c m$

|

Updated on:21/07/2023

Class 14 MATHS AREA

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Four equal circles are described about the four corners of a square so that each touches two of the others. If a side of the square is 14 cm, then the area enclosed between the circumferences of the circles is :
A $24 c m^{2}$
B $42 c m^{2}$
C $154 c m^{2}$
D $196 c m^{2}$
Question 2 - Select One
Two circles touch each other externally. The distance between their centres is 7 cm. If the radius of one circle is 4 cm, then the radius of the other circle is
A $3.5 c m$
B $3 c m$ .
C $4 c m$
D $2 c m$
Question 3 - Select One
Two circles touch each other externally. The distance between their centres is 7 cm. If the radius of one circle is 4 cm, then the radius of the other circle is
A3.5 cm
B3 cm
C4 cm
D2 cm

IBPS & SBI PREVIOUS YEAR PAPER-AREA AND PERIMETER-MCQ

Home
Ask Doubt
Profile