Statements:
All rings are circles
All squares are rings.
No.ellipse is a circle.
Conclusions: I. Some rings being ellipse is a possibility.
II. At least some circles are squres.
If only conclusion I follows
If only conclusion II follows
If either conclusion I or conclusion II follows
if neither conclusion I nor conclusion II follows
The correct Answer is:B
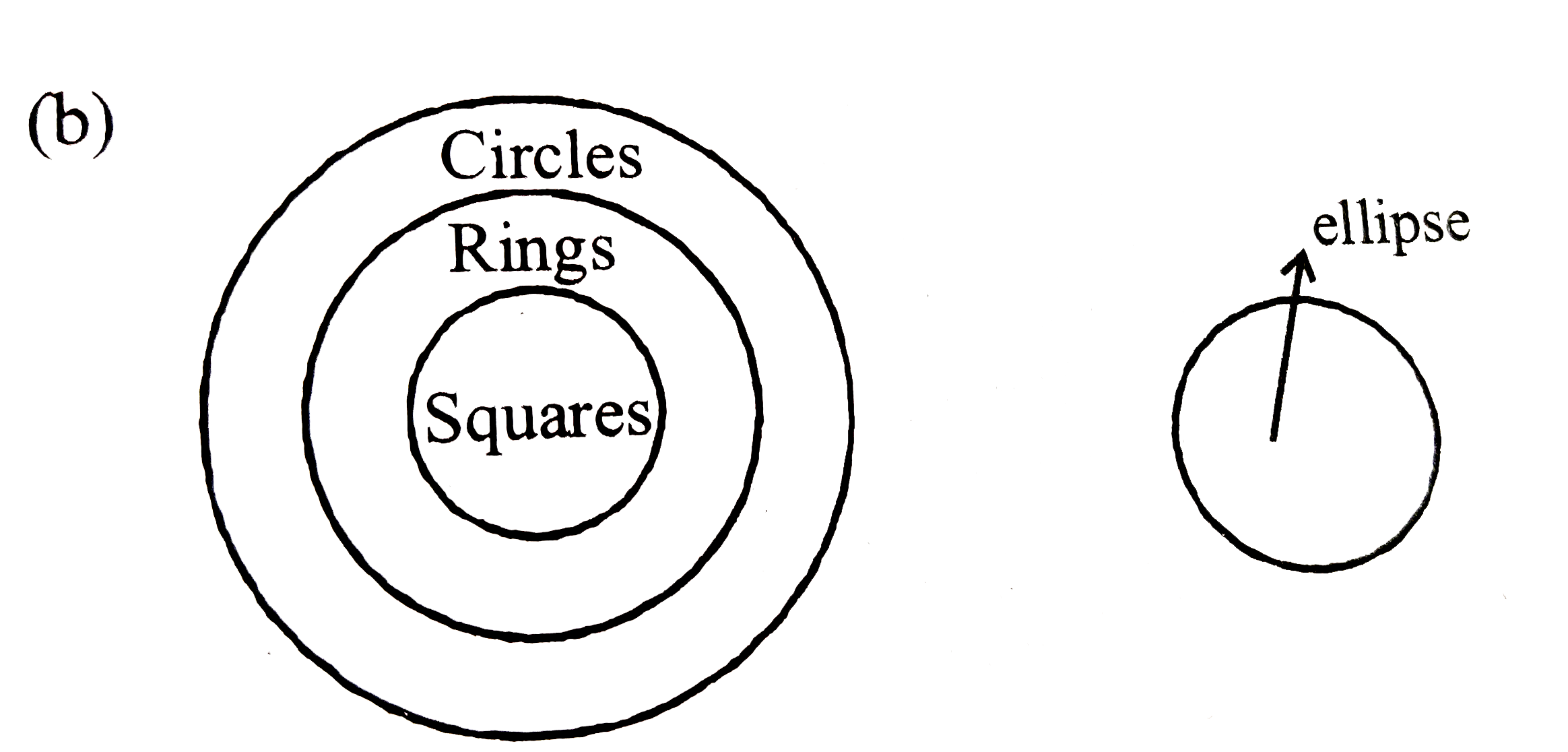
Conclusion I : False
conclusion II : True
Topper's Solved these Questions
Similar Questions
Statements: All rectangles are circles. All circles are hexagons.
Conclusions: I. Some rectangle is hexagon. II. No hexagon is rectangle.
1) If Only conclusion I follows
2)if only conclusion II follows
3) if either I or II follows
4)if neither I nor II follows
5)if both I and II followsView SolutionStatements:- All blades are sharp. Some blades are blunt. No blunt is a sword
Conclusion:- I. All sword being blades is a possibility. II. At least some blades may be swords.View Solution
Knowledge Check
- Question 1 - Select One
Statements:
All rings are circles
All squares are rings.
No.ellipse is a circle.
Conclusions: I. Some rings being ellipse is a possibility.
II. At least some circles are squres.AIf only conclusion I followsBIf only conclusion II followCIf either conclusion I or II followDIf neither conclusion I nor II follow. - Question 2 - Select One
Statements:
All stars are bottles. Some bottles are paper. No paper is a calender
Conclusions:
I. All calenders being stars is a possibility
II. Atleast some bottles are stars.AIf only conclusion I followsBIf only conclusion II followsCIf either conclusion I or conclusion II followsDif neither conclusion I nor conclusion II follows - Question 3 - Select One
Each question consists of two/three statments followed by two conclusions I and II. Consider the statements to be true even if they are in variance with the commonly known facts. Read all the conclusions and then decide which of the given conclusions logically follows from the given statements using all the statemnts together. Give answer:
All rings are Watches.
Some watch are caps.
All rings are pen.
Conclusions :
I. Some caps are rings is a possibility.
II. At least some pens are watches.AIf only conclusion I follows.BIf only conclusion II follows.CIf either conclusion I or II follows.Dlf both conclusions I and II follow.
Statements:
Some pencils are mobiles
All mobiles are grass.
All grass is green.
Conclusions:
I. All grass being pencils is a possibility.
II. No green is mobile.View SolutionStatements:
All stars are bottles. Some bottles are paper. No paper is a calender
Conclusions:
I. All stars being papers is a possibility
II. No calender is a bottleView SolutionStatements: All pages are books
Some books are words
No word is a digit
Conclusions:
I. All pages being words is a possibility
II. At least some pages are digitsView SolutionStatements:
All books are journals
All diaries are journals
Conclusions:
I. All journals are books
II. Some diaries being books is a possibilityView SolutionStatements: Some reds are green. All greens are blues. All blues are oranges. No yellow is blue.
Conclusions:
I. Some yellows are greens is a possibility
II. All yellow being oranges are a possibilityView Solution

