In a ΔABC , which one of the following is true ?
(b+c)cosA2=asin(B+C2)
(b+c)cos(B+C2)=asinA2
(b−c)cos(B−C2)=acosA2
(b−c)cosA2=asin(B−C2)
The correct Answer is:d
To determine which of the given options is true for triangle ABC, we will analyze each option step by step.
1. Understanding the Triangle Properties:
In triangle ABC, we know that the sum of the angles is A+B+C=π (or 180∘).
2. Analyzing Option 1:
- The first option states:
b+ccos(A2)=asin(B+C2)
- Since B+C=π−A, we have:
sin(B+C2)=sin(π−A2)=cos(A2)
- Thus, the equation simplifies to:
b+ccos(A2)=acos(A2)
- Rearranging gives:
b+c=a
- This is not necessarily true for all triangles, hence Option 1 is incorrect.
3. Analyzing Option 2:
- The second option states:
b+ccos(B+C2)=asin(A2)
- Using B+C=π−A:
cos(B+C2)=sin(A2)
- Thus, the equation becomes:
b+csin(A2)=asin(A2)
- Rearranging gives:
b+c=a
- This is also not necessarily true for all triangles, hence Option 2 is incorrect.
4. Analyzing Option 3:
- The third option states:
b−ccos(B−C2)=acos(A2)
- We can test this with an equilateral triangle where a=b=c.
- Substituting values leads to:
b−c⋅1=a⋅12
- This does not hold true in general, hence Option 3 is incorrect.
5. Analyzing Option 4:
- The fourth option states:
b−ccos(A2)=asin(B−C2)
- We can use the half-angle identities and properties of triangles to analyze this.
- Testing with an equilateral triangle where a=b=c:
0=0
- This holds true, and further analysis shows that it can be derived from the properties of triangles, hence Option 4 is correct.
Conclusion
After analyzing all options, we conclude that Option 4 is the correct statement for triangle ABC.
In triangle ABC, we know that the sum of the angles is A+B+C=π (or 180∘).
- The first option states:
b+ccos(A2)=asin(B+C2)
- Since B+C=π−A, we have:
sin(B+C2)=sin(π−A2)=cos(A2)
- Thus, the equation simplifies to:
b+ccos(A2)=acos(A2)
- Rearranging gives:
b+c=a
- This is not necessarily true for all triangles, hence Option 1 is incorrect.
- The second option states:
b+ccos(B+C2)=asin(A2)
- Using B+C=π−A:
cos(B+C2)=sin(A2)
- Thus, the equation becomes:
b+csin(A2)=asin(A2)
- Rearranging gives:
b+c=a
- This is also not necessarily true for all triangles, hence Option 2 is incorrect.
- The third option states:
b−ccos(B−C2)=acos(A2)
- We can test this with an equilateral triangle where a=b=c.
- Substituting values leads to:
b−c⋅1=a⋅12
- This does not hold true in general, hence Option 3 is incorrect.
- The fourth option states:
b−ccos(A2)=asin(B−C2)
- We can use the half-angle identities and properties of triangles to analyze this.
- Testing with an equilateral triangle where a=b=c:
0=0
- This holds true, and further analysis shows that it can be derived from the properties of triangles, hence Option 4 is correct.
After analyzing all options, we conclude that Option 4 is the correct statement for triangle ABC.
Topper's Solved these Questions
- BOOK - MTG-WBJEECHAPTER - SOLUTION OF TRIANGLESEXERCISE - WB JEE WORKOUT (CATEGORY 2 : single Option Correct Type )15videos
SOLUTION OF TRIANGLES
- BOOK - MTG-WBJEECHAPTER - SOLUTION OF TRIANGLESEXERCISE - WB JEE WORKOUT (CATEGORY 3 : One or More than One Option Correct Type10videos
SOLUTION OF TRIANGLES
- BOOK - MTG-WBJEECHAPTER - SETS , RELATIONS AND FUNCTIONSEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (SINGLE OPTION CORRECT TYPE)44videos
SETS , RELATIONS AND FUNCTIONS
- BOOK - MTG-WBJEECHAPTER - STATISTICS AND PROBABILITYEXERCISE - WB JEE Previous Years Questions ( CATEGORY 3 : One or More than One Option Correct Type ( 2 Marks) )3videos
STATISTICS AND PROBABILITY
Similar Questions
Knowledge Check
- Question 1 - Select One
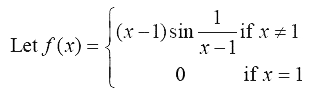
Then which one of the following is true?Af is differentiable at x = 0 and x =1Bf is differentiable at x = 0 but not at x = 1Cf is differentiable at x = 1 but not at x = 0Df is neither differentiable at x = 0 nor at x =1 - Question 2 - Select One
Which one of the following is not true?
AA−B⊆ABB'−A'⊆ACA⊆A−BDA∩B'⊆A - Question 3 - Select One
Which one of the following is not true?
AMatrix addition is associativeBMatrix addition is commutativeCMatrix multiplication is associativeDMatrix multiplication is commutative

