A current of 1A is flowing along positive x-axis through a straight wire of length 0.5m placed in a region of a magnetic field given by →B=(2ˆi+4ˆj)T. The magnitude and the direction of the force experienced by the wire respectively are
√18N, along positive z-axis
√20N, along positive x-axis
2N , along positive z-axis
4N, along positive y-axis
The correct Answer is:C
To find the magnitude and direction of the force experienced by a straight wire carrying a current in a magnetic field, we can use the formula:
→F=I→L×→B
Where:
- →F is the force on the wire,
- I is the current,
- →L is the length vector of the wire,
- →B is the magnetic field vector.
Step 1: Identify the given values
- Current, I=1A
- Length of the wire, L=0.5m (along the positive x-axis)
- Magnetic field, →B=2^i+4^jT
Step 2: Write the length vector
Since the wire is along the positive x-axis, we can express the length vector as:
→L=0.5^im
Step 3: Calculate the cross product →L×→B
Using the formula for the cross product:
→F=I(→L×→B)=1×(0.5^i×(2^i+4^j))
Step 4: Expand the cross product
Using the distributive property:
→L×→B=0.5^i×(2^i)+0.5^i×(4^j)
Calculating each term:
- ^i×^i=0
- ^i×^j=^k
So we have:
→L×→B=0+0.5×4^k=2^k
Step 5: Calculate the force
Now substituting back into the force equation:
→F=I(→L×→B)=1×(2^k)=2^kN
Step 6: Determine the magnitude and direction
- The magnitude of the force is 2N.
- The direction of the force is along the positive z-axis (since ^k indicates the z-direction).
Final Answer
The magnitude and direction of the force experienced by the wire are:
- Magnitude: 2N
- Direction: Along the positive z-axis.
---
- →F is the force on the wire,
- I is the current,
- →L is the length vector of the wire,
- →B is the magnetic field vector.
- Current, I=1A
- Length of the wire, L=0.5m (along the positive x-axis)
- Magnetic field, →B=2^i+4^jT
Since the wire is along the positive x-axis, we can express the length vector as:
→L=0.5^im
Using the formula for the cross product:
→F=I(→L×→B)=1×(0.5^i×(2^i+4^j))
Using the distributive property:
→L×→B=0.5^i×(2^i)+0.5^i×(4^j)
Calculating each term:
- ^i×^i=0
- ^i×^j=^k
→L×→B=0+0.5×4^k=2^k
Now substituting back into the force equation:
→F=I(→L×→B)=1×(2^k)=2^kN
- The magnitude of the force is 2N.
- The direction of the force is along the positive z-axis (since ^k indicates the z-direction).
The magnitude and direction of the force experienced by the wire are:
- Magnitude: 2N
- Direction: Along the positive z-axis.
Topper's Solved these Questions
- LAWS OF MOTION BOOK - MTG-WBJEECHAPTER - LAWS OF MOTION EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))
2 Videos
- MAGNETICSBOOK - MTG-WBJEECHAPTER - MAGNETICSEXERCISE - WB JEE Previous Years Questions (Category 3: One or More than one Option)
2 Videos
Similar Questions
A wire carrying a 10 A current is bent to pass through sides of a cube of side 10 cm as shown in figure. A magnetic field →B=(2ˆi−3ˆj+ˆk)T is present in the region. Then, find
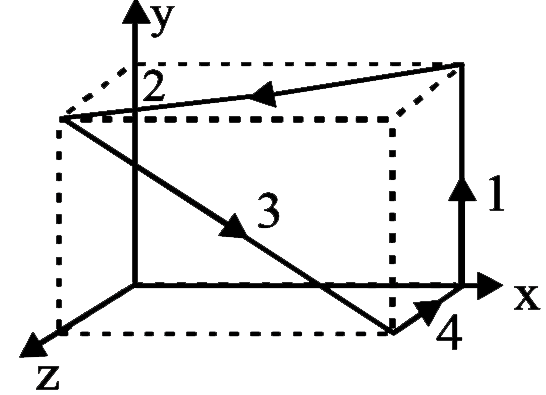
The net force on the loop
View SolutionA wire of length l carries a current I along the x-asis. A magnetic field exists which is given as →B=B0(→i+→j+→k) T. find the magnitude of the magnetic force acting on the wire.
View Solution
Knowledge Check
If →F=(5ˆi+2ˆj−4ˆk)N, the magnitude of force is
A45 NB3√5NC10 ND20 NIf →A=3ˆi−4ˆj and →B=2ˆi+16ˆj then the magnitude and direction of →A+→B will be
A5,tan−1(12/5)B10,tan−1(5/12)C13,tan−1(12/5)D12,tan−1(5/12)A current of 5 A is flowing in a wire of length 1.5 m. A force of 7.5 N acts on it when it is placed in a uniform magnetic field of 2T. The angle between the magnetic field and the direction of the current is
A60∘B90∘C30∘D45∘
A magnet of magnetic moment 50ˆiA−m2 is placed along the x-axis in a magnetic field →B=(0.5ˆi+3.0ˆj)T. The torque acting on the magnet is
View SolutionA "bar" magnet of moment ¯¯¯¯M=ˆi+ˆj is placed in a magnetic field induction →B=3ˆi+4ˆj+4ˆk.
The torque acting on the magnet is
View SolutionA magnet of magnetic moment of 50 ˆiAm2 is placed along the x - axis in magnetic field →B=(0.5ˆi+3.0ˆj)T. The torque acting on the manet is
View SolutionA magnet of magnetic moment 20ˆkAm2 is placed along the z−axis in a magnetic field →B=(0.4ˆj+0.5ˆk)T. The torque acting on the magnet is
View SolutionA dipole of magnetic moment →m=30ˆjAm2 is placed along the y-axis in a uniform magnetic field →B=(2ˆi+5ˆj)T. The torque acting on it is
View Solution
