The lower end of a capillary tube of diameter 2.0 mm is dipped 8.00cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at temperature of the experiments is 7.30×10−2Nm−1. 1 atmospheric pressure =1.01×105Pa, density of water =1000kg/m3,g=9.80ms−2. also calculate the excess pressure. Solution in Tamil
The excess pressure in a bubble of gas in a liquid is given by 2S/r where S is the surface tension of the liquid gas interface. You should note there is only one liquid surface in this case. (For a bubble of liquid in a gas, there are two liquid surfaces, so the formula for excess pressure in that case is 4S/r) THe radius of the bubble is r. Now the pressure outside the bubble P0 equals atmospheric pressure plus the pressure due to 8.00 cm of water column. That is
P0=(1.01×105Pa+0.08m×1000kgm−3×9.80ms−2)
=1.01784×105Pa
Therefore, the pressure inside the bubble is
P1=P0+2S/r
=1.01784×105Pa+(2×7.3×10−2Pam/10−3m)
=(1.01784+0.00146)×105Pa
=1.02×105Pa
Where the radius of the bubble is taken to be equal to the radius of the capillary tube. since the bubble is hemispherical (The answer has been rounded off to three significant figures.) The excess pressure in the bubble is 146 Pa.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDS BOOK - NCERT TAMILCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE
45 Videos
- LAWS OF MOTIONBOOK - NCERT TAMILCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE (V. Numerical Problems)
14 Videos
- MECHANICAL PROPERTIES OF SOLIDS BOOK - NCERT TAMILCHAPTER - MECHANICAL PROPERTIES OF SOLIDS EXERCISE - Exercises
21 Videos
Similar Questions
Why the blood pressure in humans is greater at the feet than at the brain?
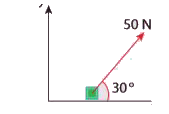
View SolutionA force of 50N act on the object of mass 20 kg. shown in the figure. Calculate the acceleration of the object in x and y directions
View SolutionA steel wire of length 4.5 m and cross-sectional area 3×10−5m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 1x10−5m2 under a given load. The ratio of the Young's modulus of steel to that of copper is
View SolutionA narrow capillary tube is dipped 10cm below water surface and a liquid bubble of radius 2mm formed at the lower end by blowing air through the tube.
a. Calculate the excess pressure due to surface tension.
b. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water?
The surface tension of water at temperature of the experiment is 7.30×10−2N/m. 1 atmospheric pressure =105Pa, density of water =1000kg/m3
View SolutionThe lower end of a capillary tube of diameter 2.0 mm is dipped 8.00cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at temperature of the experiments is 7.30×10−2Nm−1. 1 atmospheric pressure =1.01×105Pa, density of water =1000kg/m3,g=9.80ms−2. also calculate the excess pressure.
View SolutionA capillary tube is dipped in water with the lower and 10 cm below the surface. Water rises in the tube to a height of 5 cm. The pressure required to blow a bubble at the lower end of the tube will be (atmospheric pressure = 10^5 Nm^(-2) and g = 10 m//s^2 )
View Solution2.00 mm व्यास की किसी केशनली का निचला सिरा बीकर में भरे जल के पृष्ट से 8.00 cm निचे तक डुबोया जाता है। नली के जल में दुबे सिरे पर अर्घगोलीअ बुलबुला फूलने के लिए नाली के भीतर आवश्यक दाब ज्ञात कीजिये। प्रयोग के ताप पर जल का पृष्ट तनाव 7.30×10−2Nm−1 है। जल का घनत्व =1000k/m3, वायुमंडलीय दाब =1.01×105 Pa तथा g=9.80ms2|दाब आधिक्य भी परिकलित कीजिये।
View SolutionThe lower end of a capillary tube of diameter 2.00 mm is dipped 8.00 cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at the temperature of the experiments is 7.30 xx 10^(-2) "N/m" . 1 atmospheric pressure =1.01 xx 10^(5) Pa density of water =7000" kg/m"^(3), g="9.80 ms"^(-2) . Also calculate the excess pressure.
View SolutionThe lower end of a capillary tube of diameter 2.00mm is dipped 8.00cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at temperature of the experiments is 7.30×10−2Nm−1.1 atmospheric pressure =1.01×105Pa density of water =1000kg/m3,g=9.80ms−2. Also calculate the excess pressure.
View SolutionThe lower end of a capillary tube of diameter 2.00mm is dipped 8.00cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at temperature of the experiments is 7.30 times 10^2 Nm^-1 .1 atmospheric pressure =1.01 times 10^5 Pa density of water =1000 kg//m^3,g=9.80 ms^-2 . Also calculate the excess pressure.
View SolutionThe lower end of a capillary tube of diameter 2.00mm is dipped 8.00cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at temperature of the experiments is 7.30×102Nm−1.1 atmospheric pressure =1.01×105Pa density of water =1000kg/m3,g=9.80ms−2. Also calculate the excess pressure.
View SolutionThe lower end of a capillary tube of diameter 2.00mm is dipped 8.00cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at temperature of the experiments is 7.30 times 10^2 Nm^-1 .1 atmospheric pressure =1.01 times 10^5 Pa density of water =1000 kg//m^3,g=9.80 ms^-2 . Also calculate the excess pressure.
View SolutionThe lower end of a capillary tube of diameter 2.0 mm is dipped 8.00cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at temperature of the experiments is 7.30×10−2Nm−1. 1 atmospheric pressure =1.01×105Pa, density of water =1000kg/m3,g=9.80ms−2. also calculate the excess pressure.
View SolutionThe lower end of a capillary tube of diameter 2.00 mm is dipped 8.00 cm below the surface of water in a beaker . What is the pressure required in the tube in order to blow a hemispherical bubble at the end in water ? The surface tension of water at temperature of the experiments is 7.30×10−2Nm9−1.
1 atmospheric pressure =1.01×105Pa.
Density of water =1000kg/m3,g=9.80ms−2.
Also calulate the excess pressure .
View SolutionThe lower end of a capallary tube of diameter 2.50 mm is dipped 8.00 cm below the surface of water in a beaker .What is the pressure required in the tube in order to blow a hemispherical bubble at the end in water ? The surface tension of water at temperature of the experiments is 7.30×10−2Nm−1. 1 atmospheric pressure 1.01×105Pa. Density of water =1000kg/m3,g=9.80ms−2.Also calculate the excess pressure .
View SolutionThe lower end of a capillary tube of diameter 2.00 mm is dipped 8.00 cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water. [The surface tension of waterat temperature of the experiment is 7.30×10−2Nm−1. 1 atmospheric pressure = 1.01×105 Pa, density of water = 1000kgm−3,g=9.80ms−2].
View Solution
