Find the magnitude and direction of the resultant of two vectors A and B in terms of their magnitudes and angle $θ$ between them .

Text Solution

Verified by Experts

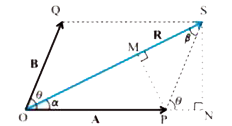
Let OP and OQ represent two vectors A and B making an angle $θ$ (Fig . 4.10) . Then , using the parallelogram method of vector addition , OS represents the resultant vector R:
R = A+B
SN is normal to OP and PM is normal to OS . From the geometry of the figure,
$O S^{2} = O N^{2} + S N^{2}$
but $O N = O P + P N = A + B cos θ$
$S N = B sin θ$
$O S^{2} = {(A + B cos θ)}^{2} + {(B sin θ)}^{2}$
or , $R^{2} = A^{2} + B^{2} + 2 A B cos θ$
$R = \sqrt{A^{2} + B^{2} + 2 A B cos θ}$
In $Δ O S N S N = O S sin α = R sin α, and$
in $Δ P S N, S N = P S sin θ = B sin θ$
Therefore , $R sin α = B sin θ$
or $\frac{R}{sin θ} = \frac{B}{sin α}$
similarly
$P M = A sin α = B sin β$
or $\frac{A}{sin β} = \frac{B}{sin α}$
or Combining Eqs . (4.24b) and (4.24c),we get
$\frac{R}{sin θ} = \frac{A}{sin β} = \frac{B}{sin α}$
Using Eq . (424a).
or , $tan α = \frac{S N}{O P + P N} = \frac{B sin θ}{A + B cos θ}$
Equation (4.24a) gives the magnitude of the resultant and Eqs . (4.24e) and (4.24f) its direction. Equantion (4.24a) is known as the Law of cosines and Eq . (4.24d) as the Law of sines.

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

NCERT TELUGU-MOTION IN A PLANE-EXCERCISES

Home
Ask Doubt
Profile