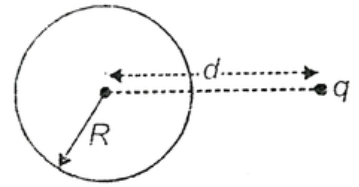
Find the electric field at the center of the sphere due to the induced charges on the surface of the sphere, as shown in Fig. 22-30.

KEY IDEA
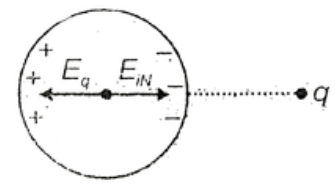
Here, we note that the induced charges will form a certain pattern on the surface of the sphere which cannot be predicted. But we can find the electric field due to q at any point. The net electric field inside the conductor is zero. This is produced by the induced charged and the external charge.
Calculations: At the center this electric field due to q in the positive direction will be (Fig. 22-31):
EQ=q4πε0d2.

Since the net electric field at the center has to be zero.
Einduced+EQ=0⇒Einduced=−q4πε0d2.
Here, the charges will be induced on the surface of the sphere, but they will not be uniformly distributed. So, we cannot apply the formula for the electric field due to a uniformly charged spherical shell.
Learn: When we say the electric field is zero, this implies that electric field should be zero inside the core of a solid metal. These are the points where the free electrons are present within the lattice. These free electrons should not experience any force.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Check points
9 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Problems
63 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
Similar Questions
A charge q kept in front of a neutal metallic sphere. Find the electric field at the centre of sphere due to the induced charges on the surface of the sphere shown.
The net electric field inside the conductor is zero. This is produced by induced charged and the external charge.

View SolutionA charge q kept in front of a neutral metallic sphere. Find the electric field at the centre of sphere due to the induced charges on the surface of the sphere shown.
Strategy : The net electric field inside the conductor is zero. This is produced by induced charges and the external charge.
View Solution
Knowledge Check
A thin conducting ring of radius R is given a charge +Q, Fig. The electric field at the center O of the ring due to the charge on the part AKB of the ring is E. The electric field at the center due to the charge on part ACDB of the ring is
 A3E along KOBE along OKCE along KOD3E along OK
A3E along KOBE along OKCE along KOD3E along OKIn the above problem, find the electric field and electric potential at the centre of the sphere due to induced charges on the sphere?
A14π∈0QR2and0B0and14π∈0QRC14π∈0QR2and14π∈0QRD0 and 0The electric field between the two spheres of a charged spheres condenser
Ais zeroBis constantCincrease with distance from centreDdecrease with distance from centre
A charge q kept in front of a neutral metallic sphere. Find the electric field at the centre of sphere due to the induced charges on the surface of the sphere shown.

Strategy : The net electric field inside the conductor is zero. Thsi is produced by induced charges and the external charge.

View SolutionA thin conducting ring of radius R is given a charge +Q, Fig. The electric field at the center O of the ring due to the charge on the part AKB of the ring is E. The electric field at the center due to the charge on part ACDB of the ring is

View SolutionElectric field due to spheres
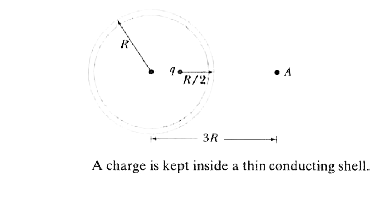
View SolutionFind the electric field at (A) (a) due to q, (b) due to charges induced on the inner surface of the shell and (c ) due to charges induced on the outer surface of the shell (Fig. 22-41).
View SolutionThe surface density on a copper sphere is σ. The electric field strength on the surface of the sphere is
View Solution
