Three particles are fixed on an x axis. Particle 1 of charge q1 is at x = -a, and particle 2 charge q2 is at x = +a. If their net electrostatic force on particle 3 of charge +Q is to be zero, what must be the ratio q1/q2 when particle 3 is at (a) x = +0.750 a and (b) x = +1.50 a ?
To solve the problem step by step, we will analyze the forces acting on the third particle (charge +Q) due to the first two particles (charges q1 and q2) at the specified positions.
Given:
- Charge q1 is located at x=−a
- Charge q2 is located at x=+a
- Charge Q is located at either x=+0.750a or x=+1.50a
Part (a): When x=+0.750a
1. Determine the distances:
- Distance from q1 to Q:
x1=0.750a−(−a)=0.750a+a=1.750a
- Distance from q2 to Q:
x2=a−0.750a=0.250a
2. Calculate the forces acting on Q:
- Force due to q1 on Q (F1):
F1=k|q1Q|(1.750a)2
- Force due to q2 on Q (F2):
F2=k|q2Q|(0.250a)2
3. Set the forces equal for equilibrium (net force = 0):
F1=F2
k|q1Q|(1.750a)2=k|q2Q|(0.250a)2
4. Cancel common terms (k and Q):
|q1|(1.750)2=|q2|(0.250)2
5. Rearranging gives the ratio:
q1q2=(1.750)2(0.250)2
=3.06250.0625=49
Part (b): When x=+1.50a
1. Determine the distances:
- Distance from q1 to Q:
x1=1.50a−(−a)=1.50a+a=2.50a
- Distance from q2 to Q:
x2=a−1.50a=−0.50a(but we consider the absolute value)
x2=1.50a−a=0.50a
2. Calculate the forces acting on Q:
- Force due to q1 on Q (F1):
F1=k|q1Q|(2.50a)2
- Force due to q2 on Q (F2):
F2=k|q2Q|(0.50a)2
3. Set the forces equal for equilibrium (net force = 0):
F1=F2
k|q1Q|(2.50a)2=k|q2Q|(0.50a)2
4. Cancel common terms (k and Q):
|q1|(2.50)2=|q2|(0.50)2
5. Rearranging gives the ratio:
q1q2=(2.50)2(0.50)2
=6.250.25=25
Final Answers:
- (a) The ratio q1q2=49
- (b) The ratio q1q2=25
- Charge q1 is located at x=−a
- Charge q2 is located at x=+a
- Charge Q is located at either x=+0.750a or x=+1.50a
- Distance from q1 to Q:
x1=0.750a−(−a)=0.750a+a=1.750a
- Distance from q2 to Q:
x2=a−0.750a=0.250a
- Force due to q1 on Q (F1):
F1=k|q1Q|(1.750a)2
- Force due to q2 on Q (F2):
F2=k|q2Q|(0.250a)2
F1=F2
k|q1Q|(1.750a)2=k|q2Q|(0.250a)2
|q1|(1.750)2=|q2|(0.250)2
q1q2=(1.750)2(0.250)2
=3.06250.0625=49
- Distance from q1 to Q:
x1=1.50a−(−a)=1.50a+a=2.50a
- Distance from q2 to Q:
x2=a−1.50a=−0.50a(but we consider the absolute value)
x2=1.50a−a=0.50a
- Force due to q1 on Q (F1):
F1=k|q1Q|(2.50a)2
- Force due to q2 on Q (F2):
F2=k|q2Q|(0.50a)2
F1=F2
k|q1Q|(2.50a)2=k|q2Q|(0.50a)2
|q1|(2.50)2=|q2|(0.50)2
q1q2=(2.50)2(0.50)2
=6.250.25=25
- (a) The ratio q1q2=49
- (b) The ratio q1q2=25
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Single Correct Choice Type)
45 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (More than one correct Type )
3 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Check points
9 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
Similar Questions
In Fig., three charged particles lie on an x axis. Particles 1 and 2 are fixed in place. Particle 3 is free to move, but the net electrostatic force on it from particles 1 and 2 happens to be zero. If 2.0L23=L12, what is the ratio q1/q2 ?
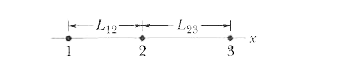
View SolutionTwo charged particles are fixed to an x axis : Particle 1 of charge q1=2.1×10−8C is at position x = 20 cm and particle 2 of charge q2=−4.00q1 is at position x = 70 cm. (a) At what coordinate on the axis (other than at infinity) is the net electric field produced by the two particles equal to zero ? (b) What is the zero-field coordinate if the particles are interchanged ?
View Solution
Knowledge Check
A charge particle q1, is at position (2, -1, 3). The electrostatic force on another charged particle q2 at (0, 0, 0) is :
Aq1q256π∈0(2ˆi−ˆj+3ˆk)Bq1q256√14π∈0(2ˆi−ˆj+3ˆk)Cq1q256π∈0(ˆj−2ˆi−3ˆk)Dq1q256√14π∈0(ˆj−2ˆi−3ˆk)A particle of mass m and charge -q circulates around a fixed charge q in a circle radius under electrostatic force. The total energy of the system is (k= (14πε0))
A−Kq22rBKq2rC−Kq2rDZero
In Fig., particle 1 of charge +6.0μC and particle 2 of charge −2.0μC are held at separation L=10.0cm on an x axis. If particle 3 of unknown charge q3 is to be located such that the net electrostatic force on it from particles 1 and 2 is zero, what must be the (a) x and (b) y coordinates of particle 3 ?
View SolutionTwo particles are fixed on an x axis. Particle 1 of charge 50μC is located at x = - 20.0 cm, particle 2 of charge Q is located at x = 3.0 cm. Particle 3 of charge magnitude 20μC is released from rest on the y axis y = 2.0 cm. What is the value of Q if the initial acceleration of particle 3 is in the positive direction of (a) the x axis and (b) the y axis ?
View SolutionA particle of mass m carrying a charge −q1 starts moving around a fixed charge +q2 along a circulare path of radius r. Find the time period of revolution T of charge −q1.
View SolutionIn Fig. four particles form a square. The charges are q1=q4=Q and q2=q3=q. (a) What is Q/q is the net electrostatic force on particles 2 and 3 is zero ? (b) Is there any value of q makes the net electrostatic force on each of the four particles zero ? Explain.

View SolutionIn Fig. 22-19, particle 1 of charge q1=5.00q and a particle 2 of charge q2+2.00q are fixed on the x-axis.
As a multiple of distance L, at what coordinate on the axis is the net electric field of the particles zero?

View SolutionTwo charged particles lie along x axis as shown in Fig. The particle with charge q2=+8μC is at x = 6.00 m, and the particle with charge q1=+2μC is at the origin. Locate the point where the resultant electric field is zero.
View Solution
