Two charged particles are attached to an x axis: Particle 1 of charge is at position x = -5.00 cm and particle 2 of charge is at position x = 10.cm. Midway between the particles, what is their net electric field in unit-vector notation ?
To find the net electric field at the midpoint between two charged particles, we can follow these steps:
Step 1: Identify the positions and charges of the particles.
- Particle 1 (P1) has a charge of q1=−4.00×10−7C located at x1=−5.00cm (or -0.05 m).
- Particle 2 (P2) has a charge of q2=+4.00×10−7C located at x2=10.00cm (or 0.10 m).
Step 2: Calculate the midpoint between the two particles.
- The distance between the two particles is d=x2−x1=0.10−(−0.05)=0.15m.
- The midpoint xm is given by:
xm=x1+x22=−0.05+0.102=0.052=0.025m(or2.5cm)
Step 3: Calculate the electric field due to each charge at the midpoint.
- The electric field E due to a point charge is given by:
E=14πϵ0|q|r2
where r is the distance from the charge to the point where the electric field is being calculated.
- Distance from P1 to midpoint:
r1=|xm−x1|=|0.025−(−0.05)|=0.075m
- Distance from P2 to midpoint:
r2=|xm−x2|=|0.025−0.10|=0.075m
Step 4: Calculate the electric field due to each charge.
- Electric field due to P1:
E1=14πϵ0|q1|r21=9×109(0.075)2×4.00×10−7
E1=9×109×4.00×10−70.005625=6.4×106N/C
Since q1 is negative, the electric field E1 points towards P1 (to the left, or negative x-direction).
- Electric field due to P2:
E2=14πϵ0|q2|r22=9×109(0.075)2×4.00×10−7
E2=9×109×4.00×10−70.005625=6.4×106N/C
Since q2 is positive, the electric field E2 points away from P2 (to the right, or positive x-direction).
Step 5: Determine the net electric field at the midpoint.
- The electric field E1 points to the left (negative x-direction) and E2 points to the right (positive x-direction).
- Since both magnitudes are equal, the net electric field Enet is:
Enet=E2−E1=6.4×106−6.4×106=0N/C
Step 6: Write the final answer in unit-vector notation.
Since the net electric field is zero, we can express it as:
Enet=0^iN/C
- Particle 1 (P1) has a charge of q1=−4.00×10−7C located at x1=−5.00cm (or -0.05 m).
- Particle 2 (P2) has a charge of q2=+4.00×10−7C located at x2=10.00cm (or 0.10 m).
- The distance between the two particles is d=x2−x1=0.10−(−0.05)=0.15m.
- The midpoint xm is given by:
xm=x1+x22=−0.05+0.102=0.052=0.025m(or2.5cm)
- The electric field E due to a point charge is given by:
E=14πϵ0|q|r2
where r is the distance from the charge to the point where the electric field is being calculated.
r1=|xm−x1|=|0.025−(−0.05)|=0.075m
r2=|xm−x2|=|0.025−0.10|=0.075m
- Electric field due to P1:
E1=14πϵ0|q1|r21=9×109(0.075)2×4.00×10−7
E1=9×109×4.00×10−70.005625=6.4×106N/C
Since q1 is negative, the electric field E1 points towards P1 (to the left, or negative x-direction).
E2=14πϵ0|q2|r22=9×109(0.075)2×4.00×10−7
E2=9×109×4.00×10−70.005625=6.4×106N/C
Since q2 is positive, the electric field E2 points away from P2 (to the right, or positive x-direction).
- The electric field E1 points to the left (negative x-direction) and E2 points to the right (positive x-direction).
- Since both magnitudes are equal, the net electric field Enet is:
Enet=E2−E1=6.4×106−6.4×106=0N/C
Since the net electric field is zero, we can express it as:
Enet=0^iN/C
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Single Correct Choice Type)
45 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (More than one correct Type )
3 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Check points
9 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
Similar Questions
Two charged particles are fixed to an x axis : Particle 1 of charge q1=2.1×10−8C is at position x = 20 cm and particle 2 of charge q2=−4.00q1 is at position x = 70 cm. (a) At what coordinate on the axis (other than at infinity) is the net electric field produced by the two particles equal to zero ? (b) What is the zero-field coordinate if the particles are interchanged ?
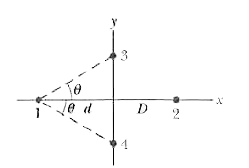
View SolutionFigure shows an arrangement of four charged particles, with angle θ=35.0∘ and distance d = 2.00 cm. Particle 2 has charge q2=+8.00×10−19C, particle 3 and 4 have charges q3=q4=−1.60×10−19C, (a) What is distance D between the origin and particle 2 if the net electrostatic force on particle 1 due to the other particles is zero ? (b) If particles 3 and 4 were moved closer to the x axis but maintained their symmetry about that axis, would the required value of D be greater than, less than, or the same as the part (a) ?
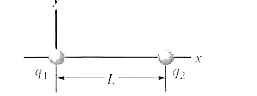
View SolutionTwo charged particles lie along x axis as shown in Fig. The particle with charge q2=+8μC is at x = 6.00 m, and the particle with charge q1=+2μC is at the origin. Locate the point where the resultant electric field is zero.
View SolutionTwo particles are fixed on an x axis. Particle 1 of charge 50μC is located at x = - 20.0 cm, particle 2 of charge Q is located at x = 3.0 cm. Particle 3 of charge magnitude 20μC is released from rest on the y axis y = 2.0 cm. What is the value of Q if the initial acceleration of particle 3 is in the positive direction of (a) the x axis and (b) the y axis ?
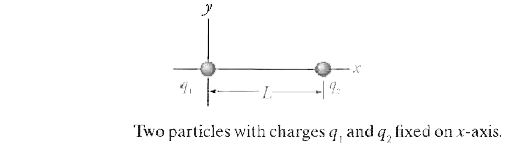
View SolutionIn Fig. 22-19, particle 1 of charge q1=5.00q and a particle 2 of charge q2+2.00q are fixed on the x-axis.
As a multiple of distance L, at what coordinate on the axis is the net electric field of the particles zero?
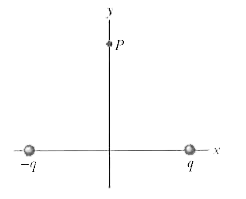
View SolutionFigure shows two charged particles on an x axis : −q=−3.20×10−19C at x=−3.00m and q=3.20×10−19C at = + 3.00 m. What are (a) magnitude and (b) direction (relative to the positive direction of the x axis) of the net electric field produced at point P at y = 4.00 m? (c ) What is the magnitude of the net field if y is doubled ?
View SolutionIn Fig. a, particle 1 (of charge q1) and particle 2 (of charge q2) are fixed in place on an x axis, 8.00 cm apart.
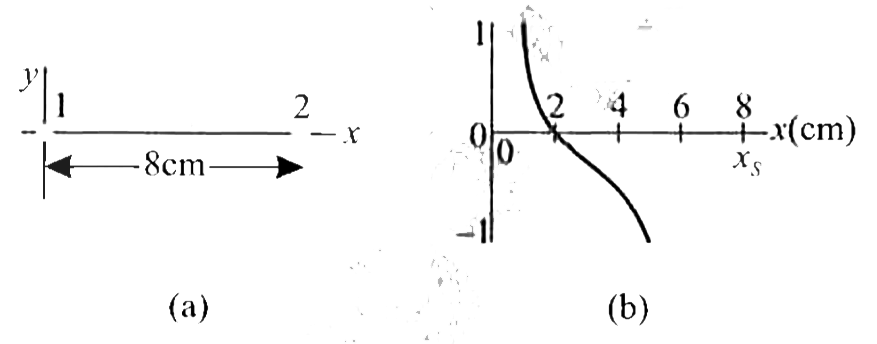
Particle 3 (of charge q3=+8.00×10−19C) is to be placed on the line between particles 1 and 2 so that they produce a net electrostatic force Fnet=2F0 on it Figure b gives the x component of that force versus the coordinate x at which particle 3 is placed. The scale of the x-axis is set by xs=8.0cm. What are (a) the sign of charge q1 and (b) the ratio q2/q1?
View SolutionIn Fig., particle 1 of charge +q and particle 2 of charge +9.00 q are held at separation L = 8.00 cm on an x axis. If particle 3 of charge q3 is to be located such that the three particles remain in place when released, what must be the (a) x and (b) y coordinates of particle 3, and (c ) the ratio q3/q ?
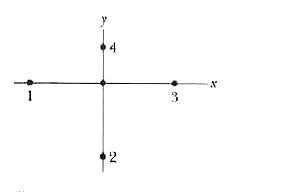
View SolutionIn Fig., particles 2 and 4, of charge -e are fixed in place on a y axis, at y2=−10.0cm and y4=5.00cm. Particles 1 and 3, of charge -e can be moved along the x axis. Particle 5, of charge +e, is fixed at the origin. Initially particle 1 is at x1=−10.0cm and particle 3 is at x3=10.0cm (a) To what x value must particle 1 be moved to rotate the direction of the net electric force →Fnet on particle 5 by 60∘ counterclockwise? (b) With particle 1 fixed at its new position, to what x value must you move particle 3 to rotate →Fnet back to its original direction ?
View SolutionTwo particles A and B having charges of +2.00×10−6C and of −4.00×10−6 respectively are held fixed at a separation of 20.0 cm . Locate the point(s) on the line AB where (a) the electric field is zero (b) the electric potential is zero.
View Solution
