The given figure shows an equilateral triangle ABC. A positive point charge |q is located at each of the three vertical A, B and C. each side of the triangle is of length a.
A point charge Q (that may be positive or negative) is placed at the mid-point between B and C.
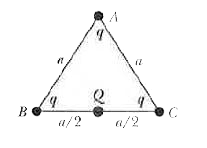
Determine an expression for the magnitude and sign of Q so that the net force on the charge at A is zero newtons.
Q=+q(3√34)
Q=−q(3√34)
Q=−q(4√34)
Q=+q(34√3)
The correct Answer is:B
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Matrix-Match)
8 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Integer Type )
3 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (More than one correct Type )
3 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
Similar Questions
ABC is an equilateral triangle. Charges +q are placed at each corner. The electric field intensity at the centroid of triangle will be
View SolutionTwo point charges +6qand−8q are placed at the vertices B and C of an equilateral triangle ABC of side a. Obtain an expression for magnitude and direction of resultant electric field at the vertex A due to these two charges.
View Solution
Knowledge Check
The given figure shows an equilateral triangle ABC. A positive point charge |q is located at each of the three vertical A, B and C. each side of the triangle is of length a.
A point charge Q (that may be positive or negative) is placed at the mid-point between B and C.
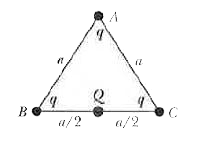
Is it possible to choose the value of Q (that is non-zero) such that the force on Q is zero ? Explain why or why not.AYes, because the forces on Q are vector and three vectors can add to zeroBNo, because the forces on q are vectors and three vectors can never add to zeroCYes, because the electric force at the mid-point between B and C is zero whether a charge is placed there or not.DNo, because a fourth charge would be needed cancel the force on Q due to the charge at A.Three charges each of magnitude q are placed at the corners of an equilateral triangle, the electrostatic force on the charge place at the centre is (each side of triangle is L)
 AZeroB14πε0q2L2C14πε03q2L2D112πε0q2L2
AZeroB14πε0q2L2C14πε03q2L2D112πε0q2L2A point charge .q. is kept at each of the vertices of an equilateral triangle having each side .a.. Total electrostatic potential energy of the system is:
A(14πε0)3q2a2B(14πε0)3qaC(14πε0)3q2aD(14πε0)3qa2
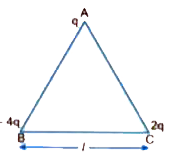
(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work done to separate the charges at infinite distance.
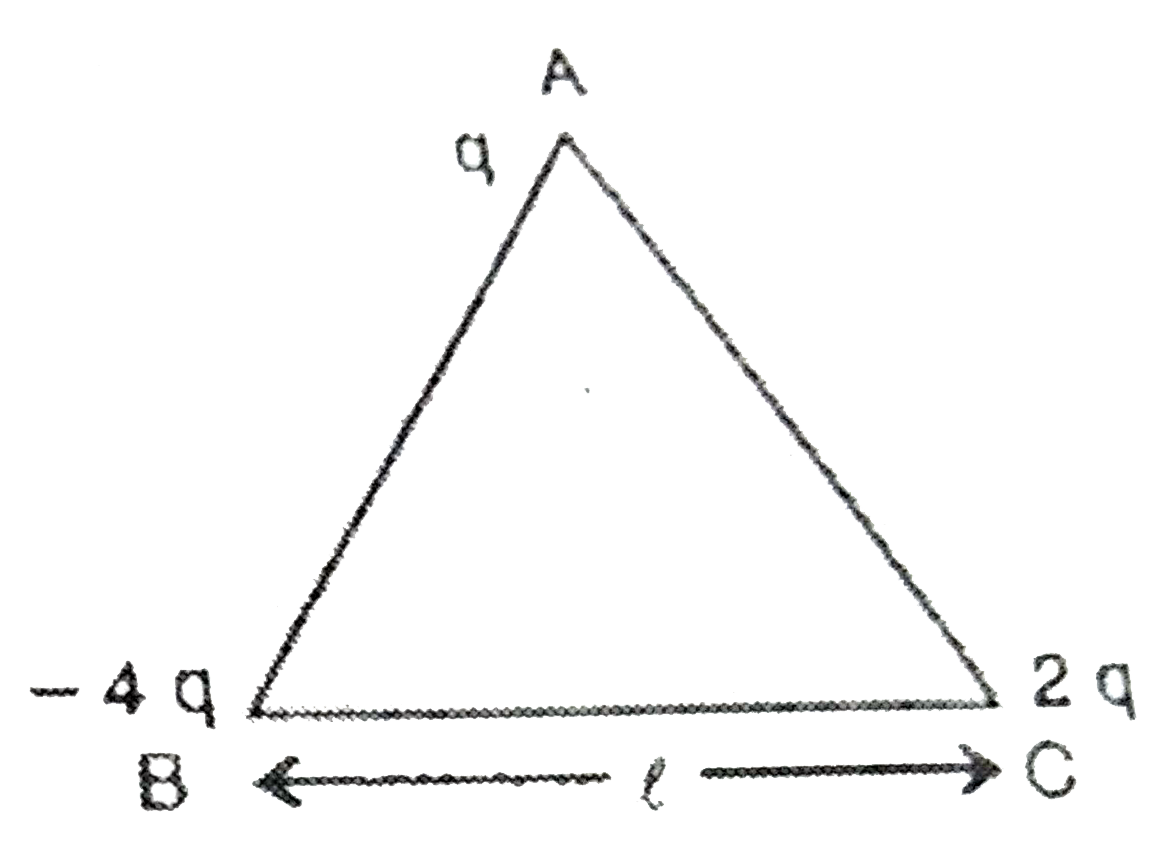
View SolutionThree point charges q,−4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the Fig. Obtain the experssion for the magnitude of the resultant electric force acting on the charge q.
View SolutionThree point charges q are placed on vertices of an equilateral triangle of side length a. The charge Q that should be kept at centroid of triangle such that the system is in equilibrium is equal to
View SolutionThree point charges + q each are kept at the vertices of an equilateral triangle of side l. Determine the magnitude and sign of charge to be kept at the centroid so that charges at the vertices remain in equillibrium.
View SolutionThree charges each of value q are placed at the corners of an equilateral triangle. A fourth charge Q is placed at the centre of the triangle. If Q=−q:
View Solution
