One end of a board of length l is hinged on top of a stone protruding from water . Length a of the board is above the point of support (Fig) . What part of the board is below the surface of the water in equilibrium state , if the density of wood is γ ?
To solve the problem, we need to analyze the forces acting on the board and apply the principles of equilibrium. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Setup
We have a board of length L that is hinged at one end on a stone above the water surface. The length a of the board is above the point of support, and we need to find the length x of the board that is submerged in water when the system is in equilibrium.
Step 2: Identify Forces Acting on the Board
1. Weight of the Board (W): The weight acts downwards at the center of mass of the board, which is at a distance L2 from the hinge. The weight can be expressed as:
W=Density of wood×Volume of board×g=γ⋅A⋅L⋅g
where A is the cross-sectional area of the board.
2. Buoyant Force (F_b): The buoyant force acts upwards on the submerged part of the board. The volume of the submerged part is A⋅x, and the buoyant force can be expressed as:
Fb=Density of water×Volume of submerged part×g=γ0⋅A⋅x⋅g
Step 3: Set Up the Torque Equation
For the board to be in equilibrium, the net torque about the hinge point must be zero. We consider the torques due to the weight of the board and the buoyant force.
1. Torque due to Weight (T_w):
Tw=W⋅(L2−a)=γ⋅A⋅L⋅g⋅(L2−a)
(acting in the clockwise direction)
2. Torque due to Buoyant Force (T_b):
Tb=Fb⋅(L−x2−a)=γ0⋅A⋅x⋅g⋅(L−x2−a)
(acting in the counterclockwise direction)
Step 4: Apply the Equilibrium Condition
Setting the net torque to zero:
Tw−Tb=0
Substituting the expressions for Tw and Tb:
γ⋅A⋅L⋅g⋅(L2−a)=γ0⋅A⋅x⋅g⋅(L−x2−a)
Step 5: Simplify the Equation
Cancel out A and g from both sides:
γL(L2−a)=γ0x(L−x2−a)
Step 6: Rearrange and Solve for x
Rearranging the equation gives us a quadratic equation in x:
γ0x(L−x2−a)−γL(L2−a)=0
Step 7: Solve the Quadratic Equation
Using the quadratic formula, we can solve for x:
x=−b±√b2−4ac2a
where a,b,c are coefficients from the rearranged equation.
Final Step: Determine the Valid Solution
After solving for x, we need to check the physical constraints of the problem to ensure that x is a valid length (i.e., 0<x<L).
We have a board of length L that is hinged at one end on a stone above the water surface. The length a of the board is above the point of support, and we need to find the length x of the board that is submerged in water when the system is in equilibrium.
1. Weight of the Board (W): The weight acts downwards at the center of mass of the board, which is at a distance L2 from the hinge. The weight can be expressed as:
W=Density of wood×Volume of board×g=γ⋅A⋅L⋅g
where A is the cross-sectional area of the board.
Fb=Density of water×Volume of submerged part×g=γ0⋅A⋅x⋅g
For the board to be in equilibrium, the net torque about the hinge point must be zero. We consider the torques due to the weight of the board and the buoyant force.
Tw=W⋅(L2−a)=γ⋅A⋅L⋅g⋅(L2−a)
(acting in the clockwise direction)
Tb=Fb⋅(L−x2−a)=γ0⋅A⋅x⋅g⋅(L−x2−a)
(acting in the counterclockwise direction)
Setting the net torque to zero:
Tw−Tb=0
Substituting the expressions for Tw and Tb:
γ⋅A⋅L⋅g⋅(L2−a)=γ0⋅A⋅x⋅g⋅(L−x2−a)
Cancel out A and g from both sides:
γL(L2−a)=γ0x(L−x2−a)
Rearranging the equation gives us a quadratic equation in x:
γ0x(L−x2−a)−γL(L2−a)=0
Using the quadratic formula, we can solve for x:
x=−b±√b2−4ac2a
where a,b,c are coefficients from the rearranged equation.
After solving for x, we need to check the physical constraints of the problem to ensure that x is a valid length (i.e., 0<x<L).
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - SAMPLE PROBLEM 14.171videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - SAMPLE PROBLEM 14.181videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - SAMPLE PROBLEM 14.151videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
ELECTROMAGNETIC WAVES
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
FORCE AND MOTION - I
Similar Questions
A rod is hinged at point O. What part of length should be submerged in water so that it remains in equilibrium, if specific gravity is 0.50?
View SolutionA uniform wooden bar of length l and mass m hinged on a vertical wall of a containing water, at one end.

3/5th part of the bar is submerged in water. Find the ratio of densities of the liquid and the bar.View Solution
Knowledge Check
- Question 1 - Select One

One end of a uniform stick having length l=1m is hung from a string as shown in figure. Length a=20 cm is above the point of suspension the length of the stick below the surface of water is [ρstick/ρliquid=0.25]Ax=0.1mBx=0.15mCx=0.2mDx=0.25m - Question 2 - Select One
A solid wooden cone has been supported by a string inside water as shown in the figure. The radius of the circular base of the cone is R and the volume of the cone is V. In equilibrium the base of the cone is at a depth H below the water surface. Density of wood is d(<ρ, density of water) Then tension in the string is
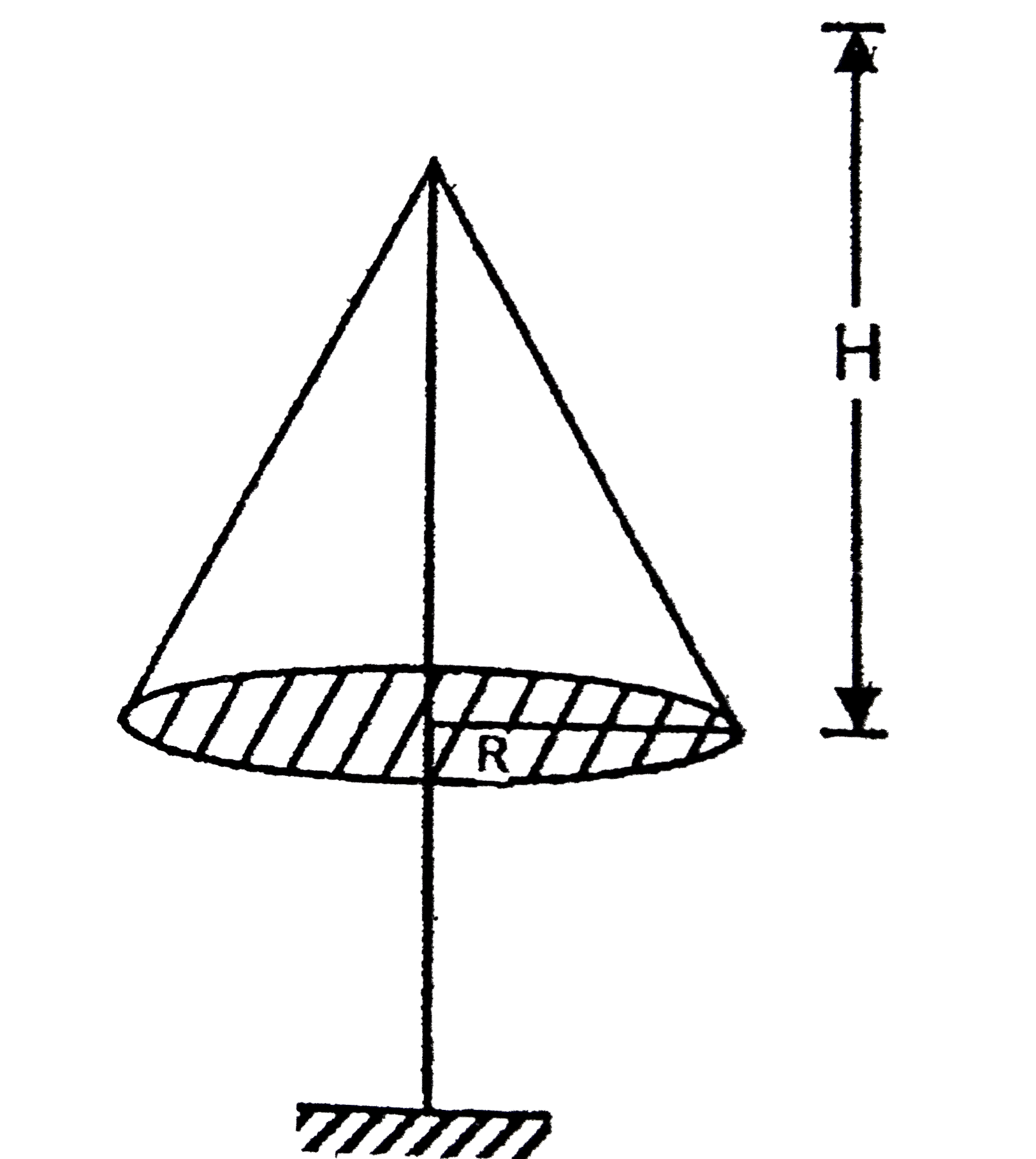 AVg(ρ−d)BVg(d+ρ)C2Vg(ρ−d)DNone of these
AVg(ρ−d)BVg(d+ρ)C2Vg(ρ−d)DNone of these - Question 3 - Select One
A uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is
 A2√5g7lB2√6g7lC√3g7lD2√gl
A2√5g7lB2√6g7lC√3g7lD2√gl
One end of a string of length 1.5 m is tied to a stone of mass 0.4 kg and the other end to a small pivot on a smooth vertical board. What is the minimum speed of the stone required at its lower most point so that the string does not slack at any point in its motion along the vertical circle ?
View SolutionA glass prism has its principal section in form of an equilateral triangle of side length l. The length of the prism is L (see fig.). The prism, with its base horizontal, is supported by a vertical spring of force constant k. Half the slant surface of the prism is submerged in water. Surface tension of water is T and contact angle between water and glass is 0∘. Density of glass is d and that of water is ρ(<d). Calculate the extension in the spring in this position of equilibrium.
 View Solution
View SolutionA wooden rod weighing 25N is mounted on a hinge below the free surface of water as shown. The rod is 3m long and uniform in cross section and the support is 1.6m below the free surface. At what angle α rod is in equilibrium? The cross-section of the rod is 9.5×10−4m2 in area. Density of water is 1000kg/m3. Assume buoyancy to act at centre of immersion. g=9.8m/s2. Also find reaction on the hinge in this position.
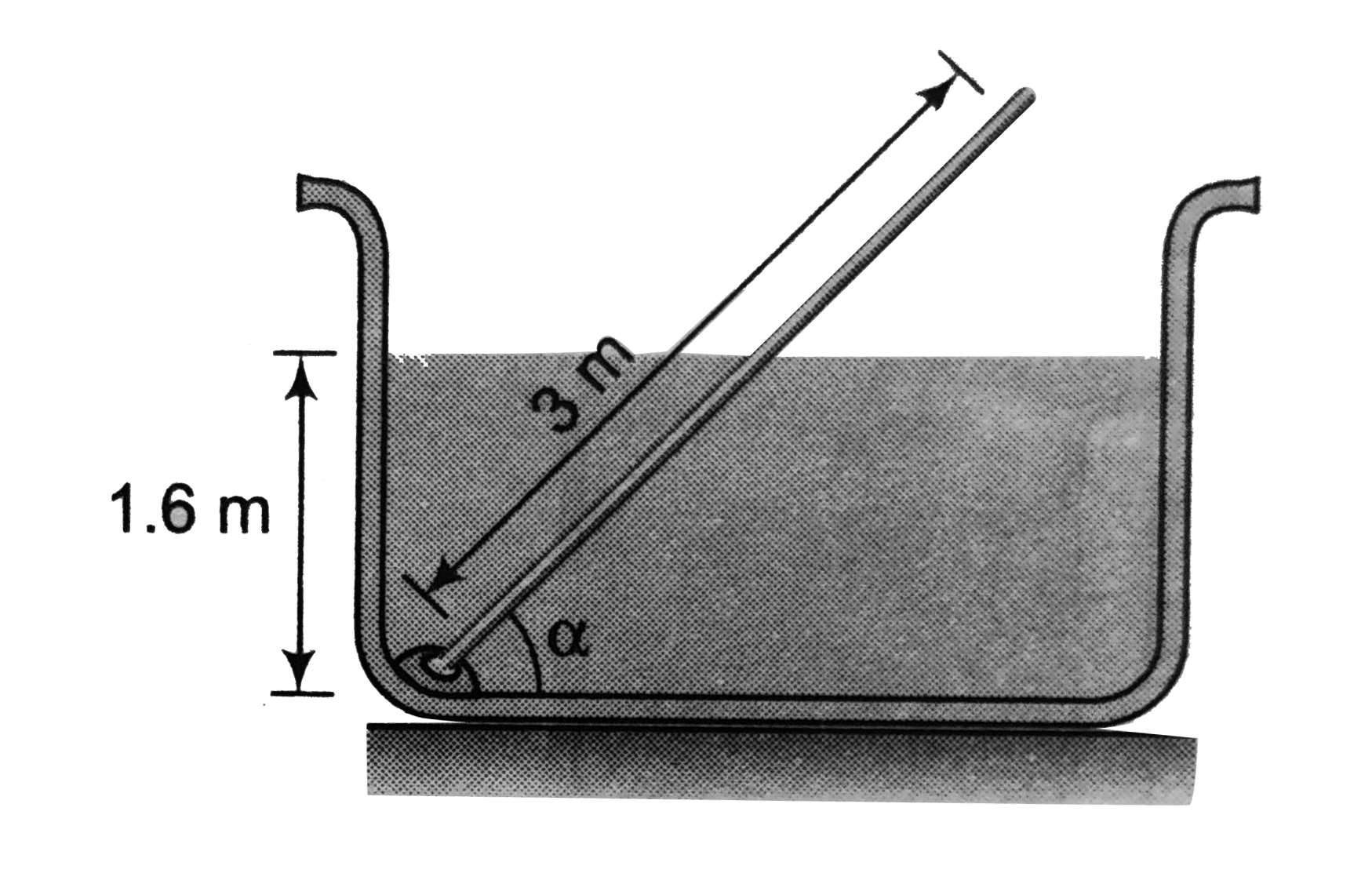 .View Solution
.View SolutionA rigid mass less rod of length L is hinged at its one end a weight W is hung at a distance l(<L) from this end.
What is force P should be applied upwards at the other end so that the rod remains in equilibrium horizontally ?
 .View Solution
.View SolutionSTATEMENT-1: One end of a string of length r is tied to a stone of mass m and the other end to a small pivot on a frictionless vertical board. The stone is whirled in a vertical circle with the pivot as the centre. The minimum speed the stone must have, when it is at the topmost point on the circle, so that the string does not slack is √gR.
because
STATEMENT-2: At the topmost point on the circle, the centripetal force is provided partly by tension in the string and partly by the weight of the stone.View Solution

