A tank has two outlets (i) a rounded orifice A of diameter D and (ii) a pipe B with well - rounded entry and of length L , as shown in Fig. For a height of water H in the tank , determine the (a) discharge from the outlets A and B , (b) velocities in the two outlets at levels 1 and 2 indicated in Fig .
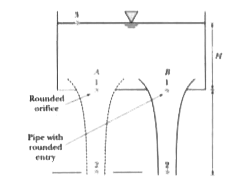
(a) Rounded orifice A : Applying Bernoulli.s equation to a point on the water surface 3 and point 1 , we get
0+0+H=p1γ+V21A2g+0
As the orifice discharges to atmosphere ,
p1γ=0 and V1A=√2gH
The discharge is ,
QA=π4D2√2gH
At point 2 , the pressure is atmospheric and hence by applying Bernoulli.s equation between points 3 and 2 , we get
0+0+(H+L)=0+V22A2g+0
or V2A=√2g(H+L)
As the discharge is QA , the diameter at 2 will be smaller than D .
(b) Pipe B : By applying Bernoulli.s equation between points 3 and 2 .
0+0+(H+L)=0+V22B2g+0
or V2B=√2g(H+L)
As the pipe size is uniform from points 1 to 2 , by continuity equation
V1B+V2B=√2g(H+L)
thus , the results are :
OrificePipeVelocity at 1√2gH√2g(H+L)Velocity at 2√2g(H+L)√2g(H+L)Discharge Qπ4D2√2gHπ4D2√2g(H+L)
Topper's Solved these Questions
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - SAMPLE PROBLEM 14.29
1 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - CHECKPOINT
8 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - SAMPLE PROBLEM 14.27
1 Videos
- ELECTROMAGNETIC WAVES BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
Similar Questions
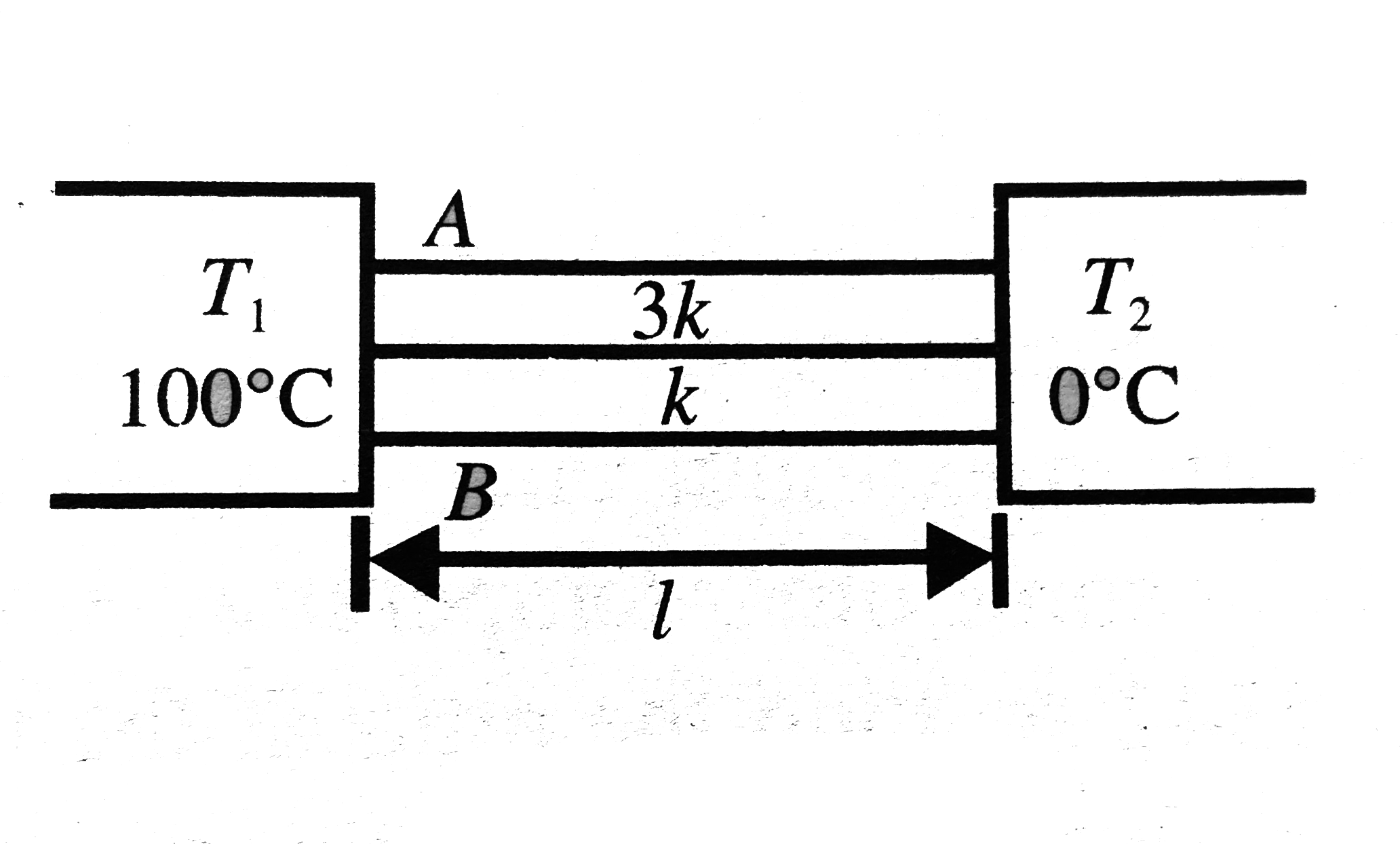
Two conductors A and B are connected in parallel as shown in Fig.
i. Determine the equivalent thermal resistance.
ii. Determine the heat current in each rod.
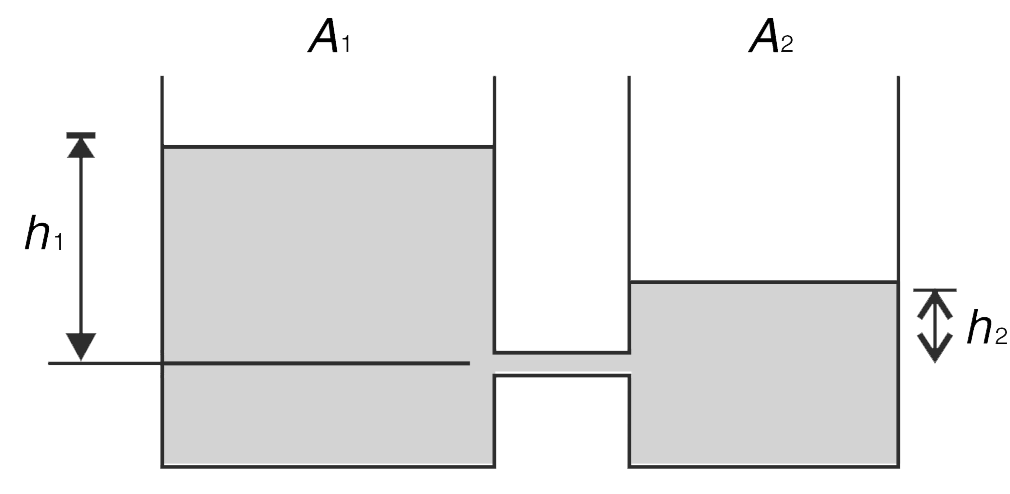
View SolutionThere are two tanks next to each other having cross sectional area A1 and A2. They are interconnected by a narrow pipe having area of cross section equal to A0. Initial height of water in the two tanks is h1 and h2 meaured from the level of the pipe. Assume that the flowis ideal and behaves in a way similar to the discharge in air. Calculate the time needed for the water level in two tanks to become same.
View Solution
Knowledge Check
A tank filled with water upto 1.25 m has two outlets (i) a rounded orifice A or area of cross section 104m2 and (ii) a pipe B with well rounded entry and of length 55 cm ,
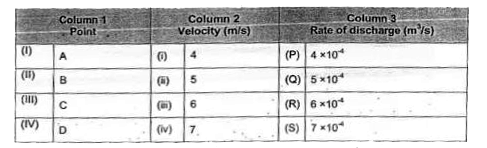
Pick the correct combination .A(III) (iii) (R )B(I) (iii) (Q )C(IV) (ii) (Q)D(IV) (i) (P)A tank filled with water upto 1.25 m has two outlets (i) a rounded orifice A or area of cross section 104m2 and (ii) a pipe B with well rounded entry and of length 55 cm ,

Pick the correct combinationA(II) (iii) (R )B(I) (iv) (S)C(IV) (I) (P)D(III) (ii) (Q)A tank filled with water upto 1.25 m has two outlets (i) a rounded orifice A or area of cross section 104m2 and (ii) a pipe B with well rounded entry and of length 55 cm ,

Pick the correct combination for list velocity .A(II) (i) (P)B(I) (ii) (Q)C(I) (i) (P)D(II) (ii) (Q)
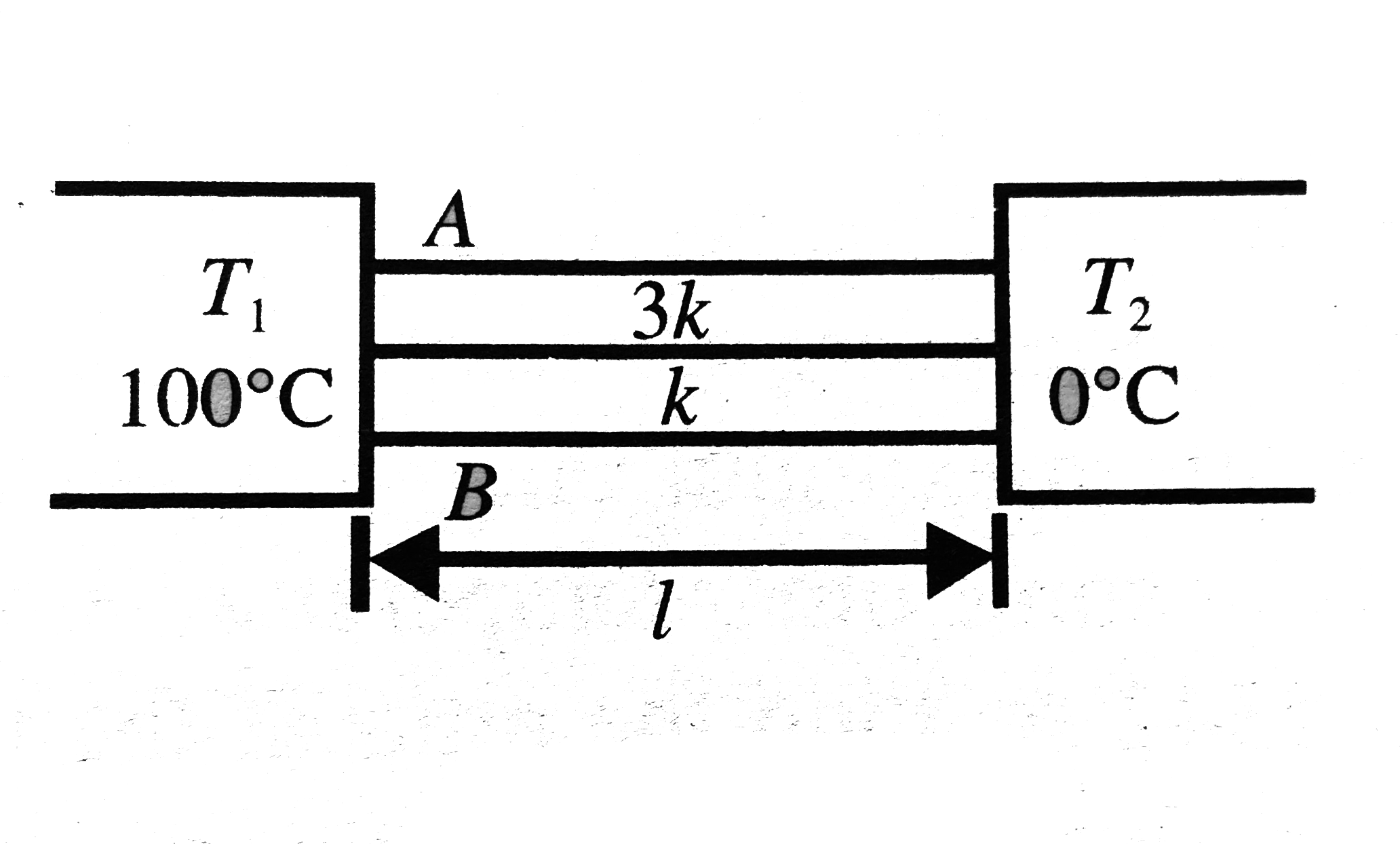
Two conductors A and B given in previous problem are connected in parallel as shown in Fig.
i. Determine the equivalent thermal resistance.
ii. Determine the heat current in each rod.
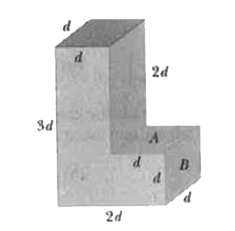
View SolutionThe L-shaped fish tank shown in Fig. is filled with water and is open at the top . Here , d = 70 m .
(a) What is the (total) force exerted by the water on face A ?
(b) What is the (total) force exerted by the water on face B ?
View SolutionA wooden cylinder of diameter 4 r, height H and density ρ/3 is kept on a hole of diameter 2 r of a tank, filled with water of density ρ as shown in the

The block in the above question is maintained by external means and the level of liquid is lowered. The height h2 when this external force reduces to zero is
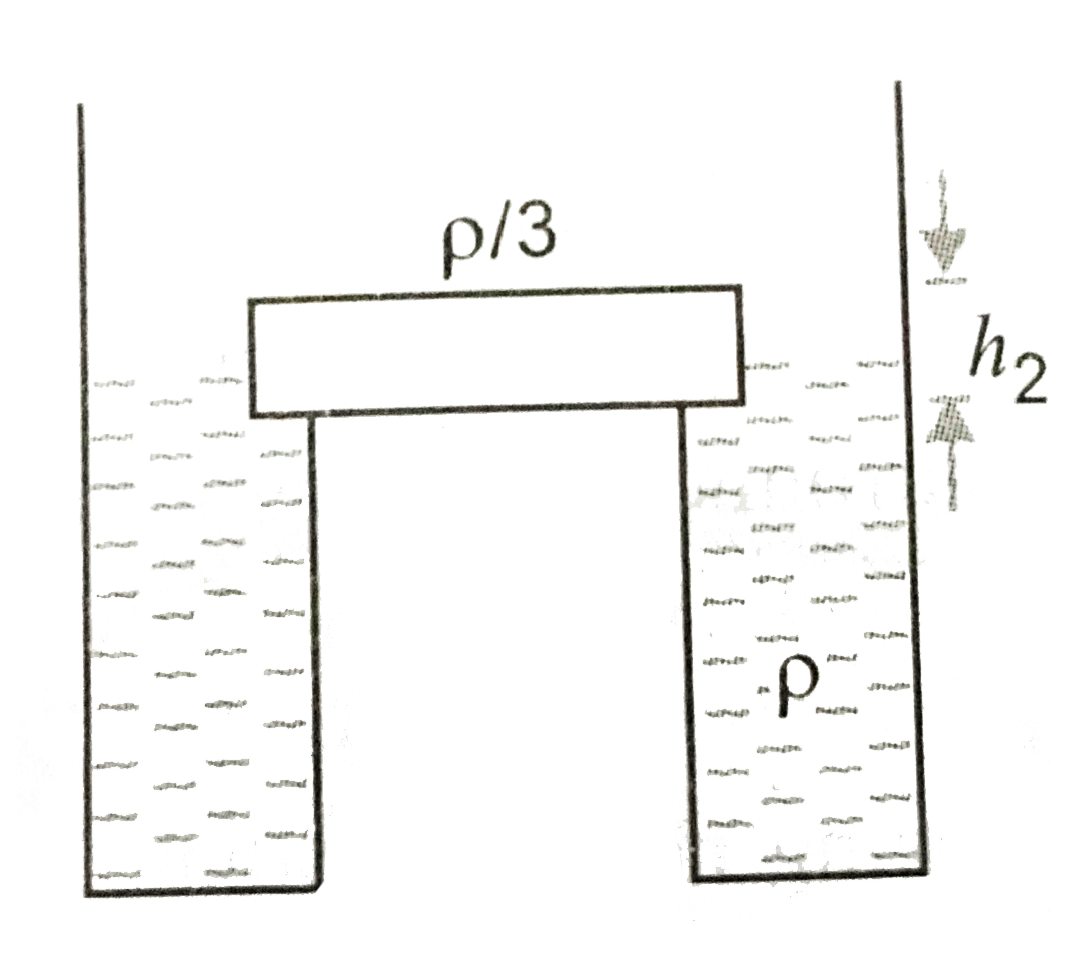
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level h2 (in situation 2), for which the block remains in its origin) position whithout the application of any external force
View Solution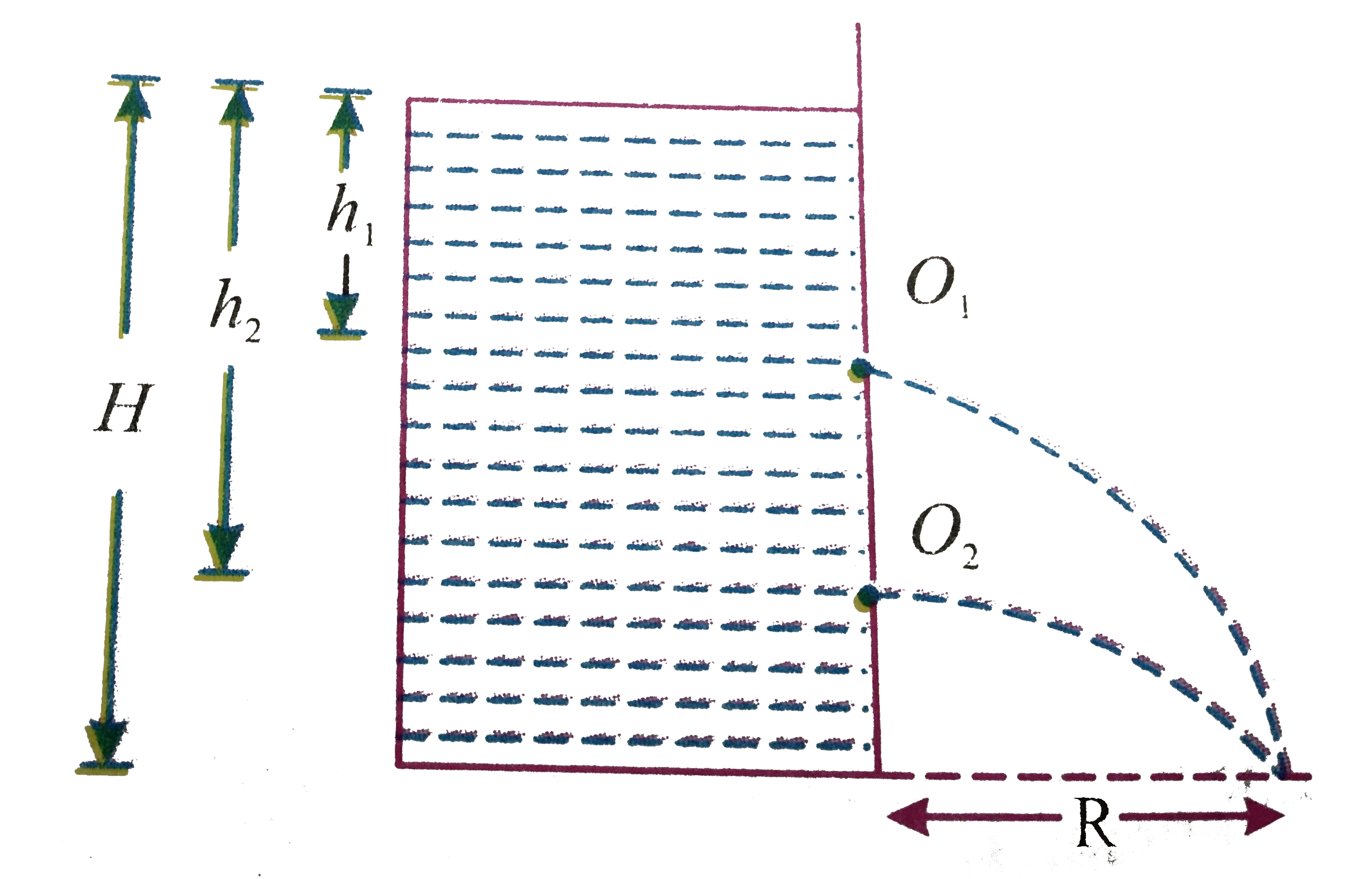
There are two holes O1 and O2 in a tank of height H. The water emerging from O1 and O2 strikes the ground at the same points as shows in fig. Then:
View Solution
