A woman is enjoying a cold drink while lying on a beach. The acceleration due to gravity at her location is 9.85 m/s8. What gauge pressure must exist in the woman's mouth if she is drinking through a straw extending 0.085 m above the surface of the drink? (Assume the drink has a density of 1015 kg/m3.)
850 Pa
970 Pa
1100 Pa
2100 Pa
The correct Answer is:A
To find the gauge pressure that must exist in the woman's mouth while drinking through a straw, we can use the hydrostatic pressure formula, which relates the pressure difference to the height of the liquid column.
1. Identify the given values:
- Density of the drink, ρ=1015kg/m3
- Acceleration due to gravity, g=9.85m/s2
- Height of the straw above the surface of the drink, h=0.085m
2. Use the hydrostatic pressure formula:
The gauge pressure P at the height of the straw can be calculated using the formula:
P=ρgh
3. Substitute the known values into the formula:
P=1015kg/m3×9.85m/s2×0.085m
4. Calculate the pressure:
- First, calculate ρg:
ρg=1015×9.85=10000.75N/m3
- Now multiply by h:
P=10000.75N/m3×0.085m=850.06Pa
5. Round to appropriate significant figures:
The gauge pressure is approximately:
P≈850Pa
Final Answer:
The gauge pressure that must exist in the woman's mouth is approximately 850 Pascal.
---
- Density of the drink, ρ=1015kg/m3
- Acceleration due to gravity, g=9.85m/s2
- Height of the straw above the surface of the drink, h=0.085m
The gauge pressure P at the height of the straw can be calculated using the formula:
P=ρgh
P=1015kg/m3×9.85m/s2×0.085m
- First, calculate ρg:
ρg=1015×9.85=10000.75N/m3
- Now multiply by h:
P=10000.75N/m3×0.085m=850.06Pa
The gauge pressure is approximately:
P≈850Pa
The gauge pressure that must exist in the woman's mouth is approximately 850 Pascal.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type )10videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (Linked Comprehension )9videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PROBLEMS68videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
ELECTROMAGNETIC WAVES
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
FORCE AND MOTION - I
Similar Questions
Blood pressure in Argentinosaurus. (a) If this long-necked, gigantic sauropod had a head height of 18 m and a heart height of 8.0 m, what (hydrostatic) gauge pressure in its blood was required at the heart such that the blood pressure at the brain was 80 torr (just enough to perfuse the brain with blood)? Assume the blood had a density of 1.06×10kg/m3. (b) What was the blood pressure (in torr or mm Hg) at the feet?
View SolutionA 400 kg ice boat moves on runners on essentially frictionless ice.A steady wind blows,applying a constant force to the sail. At the end of 8.0 sec run,the acceleration is 0.5ms2. (a) What was the acceleration at the beginning of the run? (b) What was the force due to the wind ? (c) What retarding force must be applied at the end of 4.0 sec to bring the ice boat to rest by the end of the next 4 sec ? (assume boat was at rest at time t = 0)
View Solution
Knowledge Check
- Question 1 - Select One
Swimming is an interesting sport, and one that relaxes us also. Normally and average human being would drown in water.As a person goes inside water , the water exert a force on it in upwared direction. This force is called buyont froce. The force is given by V dg, where d is density of water, V is volume of body inside water and g is acceleration due to gravity. normally, this force is lesser than this weight. so the man pushes water to get an additional force on himself. this effort is known as swimming. assume water has a density of 1000kg/m3
A man of mass 50 kg has a volume of 0.045m3. how much force should be apply on water to just stay afloat?A50 N downB50 N upC100 N downD10 0 N up - Question 2 - Select One
The surface tension of water is 0.072 N/m. The height to which water will rise in a capillary tube of bore diameter 0.048 cm will be (Angle of contact of water is zero , acceleration due to gravity is 10 m/s2 and density of water =1000 kg/m3 ).
A6 cmB8 cmC4 cmD10 cm - Question 3 - Select One
When a particle is undergoing motion, the diplacement of the particle has a magnitude that is equal to or smaller than the total distance travelled by the particle. In many cases the displacement of the particle may actually be zero, while the distance travelled by it is non-zero. Both these quantities, however depend on the frame of reference in which motion of the particle is being observed. Consider a particle which is projected in the earth's gravitational field, close to its surface, with a speed of 100√2m/s, at an angle of 45∘ with the horizontal in the eastward direction. Ignore air resistance and assume that the acceleration due to gravity is 10m/s2.
The motion of the particle is observed in two different frames: one in the ground frame (A) and another frame (B), in which the horizontal component of the displacement is always zero. Two observers locates in these frames ill agree on :-AThe total distance travelled by the particleBThe horizontal range of the particleCThe maximum height risen by the particleDNone of these
A cylindrical furnace has height (H) and diameter (D) both 1 m. It is maintained at temperature 360 K. The air gets heated inside the furnace at constant pressure P_α, and its temperature becomes T = 360K The hot air with density ρ rises up a vertical chimney of diameter d = 0.1 m and height h = 9 m above the furnace and exits the chimney (see the figure). As a result, atmospheric air of density ρα=1.2kgm−3, pressure Pα, and temperature Tα = 300K enters the furnace. Assume air as an ideal gas, neglect the variations in ρ and T inside the chimney and the furnace. Also ignore the viscous effects.
[Given: The acceleration due to gravity g = 10ms−2 and π = 3.14 ]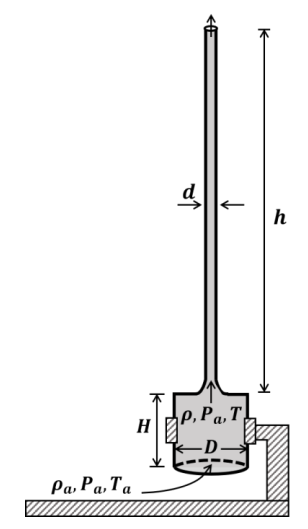
When the chimney is closed using a cap at the top, a pressure difference ΔP develops between the top and the bottom surfaces of the cap. If the changes in the temperature and density of the hot air, due to the stoppage of air flow, are negligible then the value of ΔP is _________Nm^(-2)View SolutionEverybody, when free, falls towards the centre of earth with an acceleration =g, which is called acceleration due to gravity. The value of g on the surface of earth is, g=GMR2=9.8m/s2. It is a vector, directed always the centre of earth. The value of g does not depend upon shape, size or mass of the body. Rether, it depends on mass and size of earth (or planet due to which there is a gravity pull).
Read the above passesge and answer the following questions :
(i) A piece of stone and a feather are dropped together in space from the same height. which one will strike the ground first ? (ii) The mass of a planet is 18th the mass of earth and its diameter is 56 the diameter of earth. What is the value of 'g' on the surface of this planet.
(iii) What does the concept of free fall imply in day to day life?View SolutionA woman is running through rain at a speed of 5.00 m/s. Rain is falling vertically at a speed of 20.0 m/s. (a) What is the velocity of the rain relative to the woman? (b) How far in front of her would an umbrella have to extend to keep the rain off if she holds the umbrella 1.50 m above her feet?
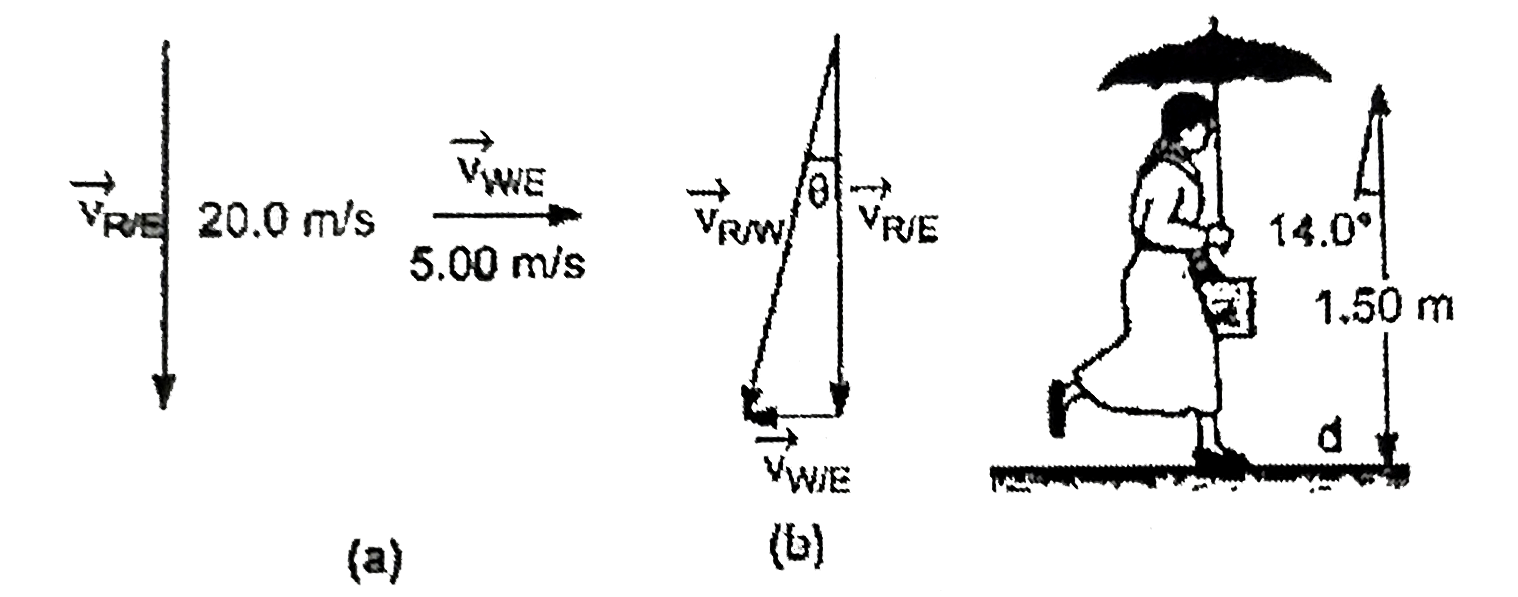 View Solution
View SolutionA 62 kg woman is a passenger in a “rotor ride” at an amuse ment park. A drum of radius 5.0 m is spun with an angular velocity of 25 rpm. The woman is pressed against the wall of the rotatingdrum as shown in figure (a) Calculate the normal force of the drum of the woman (the centripetal force that prevents her from leaving her circular path). (b) While the drum rotates, the floor is lowered. A vertical static friction force supports the woman’s weight. What must the coefficient of friction be to support her weight
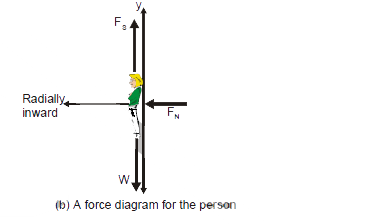 View Solution
View SolutionThe U-tube acts as a water siphon. The bend in the tube is 1m above the water surface. The tube outlet is 7m below the water surface. The water issues from the bottom of the siphon as a free jet at atmospheric pressure. Determine the speed of the free jet and the minimum absolute pressure of the water in the bend. Given atmospheric pressure =1.01×105N/m2,g=9.8m/s2 and density of water =103kg/m3
 .View Solution
.View Solution

