Water flows through a pipe of diameter 8.0 cm with a speed of 10.0 m/s . It then enters a smaller pipe of diameter 3.0 cm . What is the speed of the water as it flows through the smaller pipe ?
1.4 m/s
71 m/s
2.8 m/s
54 m/s
The correct Answer is:B
To solve the problem of water flowing through pipes of different diameters, we will use the principle of conservation of mass, specifically the equation of continuity for incompressible fluids. The equation states that the mass flow rate must remain constant throughout the flow.
1. Identify Given Values:
- Diameter of the larger pipe (D1) = 8.0 cm
- Speed of water in the larger pipe (V1) = 10.0 m/s
- Diameter of the smaller pipe (D2) = 3.0 cm
2. Convert Diameters to Meters:
- D1 = 8.0 cm = 0.08 m
- D2 = 3.0 cm = 0.03 m
3. Calculate Cross-Sectional Areas:
- The cross-sectional area (A) of a circular pipe is given by the formula:
A=π4D2
- For the larger pipe (A1):
A1=π4(0.08)2=π4×0.0064=0.0050265m2
- For the smaller pipe (A2):
A2=π4(0.03)2=π4×0.0009=0.0007069m2
4. Apply the Equation of Continuity:
- According to the equation of continuity:
A1⋅V1=A2⋅V2
- Rearranging to find V2:
V2=A1⋅V1A2
5. Substitute the Values:
- Substitute A1, V1, and A2 into the equation:
V2=0.0050265⋅10.00.0007069
6. Calculate V2:
- Performing the calculation:
V2=0.0502650.0007069≈71.1m/s
7. Conclusion:
- The speed of the water as it flows through the smaller pipe is approximately 71.1 m/s.
- Diameter of the larger pipe (D1) = 8.0 cm
- Speed of water in the larger pipe (V1) = 10.0 m/s
- Diameter of the smaller pipe (D2) = 3.0 cm
- D1 = 8.0 cm = 0.08 m
- D2 = 3.0 cm = 0.03 m
- The cross-sectional area (A) of a circular pipe is given by the formula:
A=π4D2
- For the larger pipe (A1):
A1=π4(0.08)2=π4×0.0064=0.0050265m2
- For the smaller pipe (A2):
A2=π4(0.03)2=π4×0.0009=0.0007069m2
- According to the equation of continuity:
A1⋅V1=A2⋅V2
- Rearranging to find V2:
V2=A1⋅V1A2
- Substitute A1, V1, and A2 into the equation:
V2=0.0050265⋅10.00.0007069
- Performing the calculation:
V2=0.0502650.0007069≈71.1m/s
- The speed of the water as it flows through the smaller pipe is approximately 71.1 m/s.
Topper's Solved these Questions
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type )
10 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (Linked Comprehension )
9 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PROBLEMS
68 Videos
- ELECTROMAGNETIC WAVES BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
Similar Questions
Water flow througyh a horizontal pipe whose internal diameter is 2.0cm at a speed of 1.0ms−1 What should be the diameter of the nozzle, If the water is to emerge at a speed of 4.0ms−1?
View SolutionWater is flowing though a cylindrical pipe of cross -sectional area 0.04 πm2 at a speed of1.0ms−1 If the diameter of the pipe is halved ,then find the speed of flow of water through it .
View Solution
Knowledge Check
Water is flowing in a pipe of diameter 4 cm with a velocity 3m/s . The water then enters into a tube of diameter 2 cm . The velocity of water in the other pipe is
A3m/sB6m/sC12m/sD8m/sWater enters a pipe of diameter 3.0 cm with a velocity of 3.0 m/s . The water encounters a construction where its velocity is 12 m/s . What is the diameter of the constricted portion of the pipe ?
A0.33 cmB0.75 cmC1.0 cmD1.5 cmWater is flowign through a cylindrical pipe of cross section area 0.09πm2 at a speed of 1.0 m/s. If the diameter of the pipe is halved, then find the speed of flow of water through it
A8.0 m/sB3.0m/sC4.0m/sD6.0m/s
In Fig , water flows through a pipe that tapers from radius r1=0.020 m where the water has a uniform speed v1=1.5 m/s , to a radius r2=0.010 m . What is the speed in the smaller pipe ?
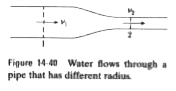
View SolutionThe water entering a hauze flows with a speed of 0.1ms−1 through a pipe of 21 mm inside diameter .What is the speed of water at a point ,where pipe tapers to a diameter of 7mm?
View SolutionA horizontal pipe of cross-section diameter 5cm carries water at a speed of 4ms−1. The pipe is connected to a smaller pipe with a cross-sectional diameter 4cm. The velocity of water through the smaller pipe is
View SolutionA horizontal pipe of cross sectional diameter 5 cm carries water at a velocity of 4m/s. The pipe is connected to a smaller pipe with a cross-sectional diameter 4 cm. The velocity of water through the smaller pipe is:
View SolutionA horizontal pipe of cross sectional diameter 5 cm carries water at a velocity of 4m/s. The pipe is connected to a smaller pipe with a cross-sectional diameter 4 cm. The velocity of water through the smaller pipe is:
View Solution
