A sinusoidal wave of angular frequency 1200 rad/s and amplitude 3.00 mm is sent along a cord with linear density 2.00 g/m and tension 1200 N. What is the average rate at which energy is transported by the wave to the opposite end of the cord?
The correct Answer is:10
To find the average rate at which energy is transported by the wave along the cord, we can use the formula for the power transmitted by a sinusoidal wave. The average power P transmitted by a wave on a string is given by:
P=12μω2A2v
Where:
- μ is the linear density of the cord (in kg/m),
- ω is the angular frequency (in rad/s),
- A is the amplitude of the wave (in m),
- v is the wave speed (in m/s).
Step 1: Convert linear density to kg/m
The linear density given is 2.00 g/m. We need to convert this to kg/m:
μ=2.00g/m=2.00×10−3kg/m
Step 2: Calculate the wave speed v
The wave speed v can be calculated using the formula:
v=√Tμ
Where T is the tension in the cord (1200 N). Plugging in the values:
v=√1200N2.00×10−3kg/m=√600000≈774.6m/s
Step 3: Calculate the average power P
Now we can substitute the values into the power formula. First, we need the angular frequency ω and the amplitude A:
- Given ω=1200rad/s
- Given A=3.00mm=3.00×10−3m
Now, substituting these values into the power formula:
P=12μω2A2v
Calculating ω2 and A2:
ω2=(1200)2=1440000rad2/s2
A2=(3.00×10−3)2=9.00×10−6m2
Now substituting all values into the power formula:
P=12(2.00×10−3)(1440000)(9.00×10−6)(774.6)
Calculating step by step:
1. Calculate 12×2.00×10−3=1.00×10−3
2. Calculate 1.00×10−3×1440000=1440
3. Calculate 1440×9.00×10−6=0.01296
4. Finally, calculate 0.01296×774.6≈10.05W
Final Answer
The average rate at which energy is transported by the wave to the opposite end of the cord is approximately:
P≈10.05W
- μ is the linear density of the cord (in kg/m),
- ω is the angular frequency (in rad/s),
- A is the amplitude of the wave (in m),
- v is the wave speed (in m/s).
The linear density given is 2.00 g/m. We need to convert this to kg/m:
The wave speed v can be calculated using the formula:
Now we can substitute the values into the power formula. First, we need the angular frequency ω and the amplitude A:
- Given A=3.00mm=3.00×10−3m
A2=(3.00×10−3)2=9.00×10−6m2
2. Calculate 1.00×10−3×1440000=1440
3. Calculate 1440×9.00×10−6=0.01296
4. Finally, calculate 0.01296×774.6≈10.05W
The average rate at which energy is transported by the wave to the opposite end of the cord is approximately:
Topper's Solved these Questions
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Matrix -Match)
7 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
5 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
Similar Questions
A sinusoidal wave of angular frequency 1200 rad/s and amplitude 3.00 mm is sent along a cord with linear density 4.00 g/m and tension 1200 N. (a) What is the average rate at which energy is transported by the wave to the opposite end of the cord? (b) If simultaneously, an identical wave travels along an adjacent identical cord, what is the total average rate at which energy is transported to the opposite ends of the two cords by the waves? IT, instead, those two Waves are sent along the same cuid simultaneously, what is the tolal average rate at which they transport energy when their phase difference is (c) 0, (d) 0.4πrad, and (e) π rad?
View SolutionA sound source sends a sinusoidal sound wave of angular frequency 3000 rad/s and amplitude 10.0 nm through a tube of air. The internal radius of the tube is 2.00 cm. (a) What is the average rate at which energy (the sum of the kinetic and potential energies) is transported to the opposite end of the tube? (b) If, simultaneously, an identical wave travels along an adjacent, identical tube, what is the total average rate at which energy is transported to the opposite ends of the two tubes by the waves? If, instead, those two waves are sent along the same tube simultaneously, what is the total average rate at which they transport energy when their phase difference is (c) 0, (d) 0.40π rad, and (e) π rad?
View SolutionA long wire PQR is made by joining two wires PQandQR of equal radii . Pq has length 4.8mandmass0.06kg. QR has a length 2.56m and mass 0.2kg. The wire PQR is under a tension of 80N . A sinusoidal wave pulse of amplitude 3.5cm is sent along the wire PQ from the end? No power is dissipated during the propagation of the wave - pulse . Calculate
(a) The time taken by the wave pulse to reach the order end R of the wire , and
(b) The amplitude of the reflected and transmitted wave pulses after the incident wave pulse crosses the joint Q.
View SolutionA sound wave of frequency 280 Hz has an intensity of 1.00W/m2 ? What is the amplitude of the air oscillations caused by this wave?
View SolutionA simple harmonic oscillator at the point x=0 genrates a wave on a rope. The oscillator operates at a frequency of 40.0 Hz and with an amplitude of 3.00 cm. the rope has a linear mass density of 50.0g/m and is strectches with a tension of 5.00 N. (a) determine the speed of the wave. (b) find the wavelength. (c ) write the wave function y(x,t) for the wave, Assume that the oscillator has its maximum upward displacement at time t=0. (d) find the maximum transverse acceleration at time t=0. (d) find the maximum transverse of points on the rope. (e) in the discussion of transverse waves in this chapter, the force of gravity was ignored. is that a reasonable assumption for this wave? explain.
View SolutionA long wire PQR is made by joining two wires PQ and QR of equal radii PQ has length 4.8m and mass 0.06kg. QR has length 2.56m and mass 0.2kg. The wire PQR is under a tension of 80N. A sinusoidal wave-pulse of amplitude 3.5cm is sent along the wire PQ from end P. No power is dissipated during the propagation of the wave-pulse. caculate,
(a) the time taken by the wave-pulse to reach the other end R of the wire, and
(b) the amplitude of the reflected and transmitted wave-pulse after the incident wave-pulse crosses the jjoint Q.
View SolutionA 200Hz wave with amplitude 1mm travels on a long string of linear mass density 6g/m keep under a tension of 60N.
(a) Find the average power transmitted across a given point on the string.
(b) Find the total energy associated with the wave in a 2.0m long portion of the string.
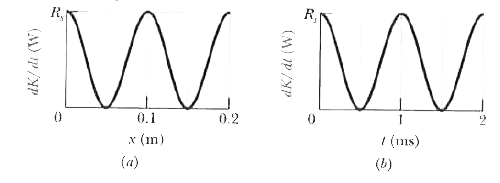
View SolutionA sinusoidal wave is sent along a string with a linear density of 5.0 g/m. As it travels, the kinetic energies of the mass elements along the string vary Figure 10-49a gives the rate dk/dt at which kinetic energy passes through the string elements at a particular instant, plotted as a function of distance x along the string. Figure 1649b is similar except that it gives the rate at which kinetic energy passes through a particular mass element at a particular location) plotted as a function of time. For botle figures the scale in the vertical (rate) axis is set by Rs=10W. What is the amplitude of the wave?
View SolutionA transverse wave of wavelength 50 cm is travelling towards+vex-axis along a string whose linear density is 0.05g/cm. The tension in the string is 450 N. At t=0,the particle at x=0 is passing through its mean position wave. The amplitude of the wave is 2.5 cm.
View SolutionIn a plane e.m.wave, the electric field oscillates sinusoidally at a frequency 2×1010Hz and amplitude 45Vm−1.
(a) What is the wavelength of wave?
(b) What is the amplitude of the oscillating magnetic field?
(c) Show that the average energy density of the electric field →E equals to the average energy density of the magnetic field →B.
View Solution
