25.5 g of H2O2 solution on decomposition gave 1.68 L of O2 at STP. The percentage strength by weight of the solution is Solution in Telugu
30
10
20
25
The correct Answer is:C
Step by step video, text & image solution for 25.5 g of H_(2)O_(2) solution on decomposition gave 1.68 L of O_(2) at STP. The percentage strength by weight of the solution is by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - STOICHIOMETRYEXERCISE - LECTURE SHEET ( EXERCISE III MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)4videos
STOICHIOMETRY
- BOOK - AAKASH SERIESCHAPTER - STOICHIOMETRYEXERCISE - LECTURE SHEET ( EXERCISE III LINKED COMPREHENSION TYPE QUESTIONS)5videos
STOICHIOMETRY
- BOOK - AAKASH SERIESCHAPTER - STOICHIOMETRYEXERCISE - LECTURE SHEET ( EXERCISE II INTEGER TYPE QUESTIONS)8videos
STOICHIOMETRY
- BOOK - AAKASH SERIESCHAPTER - STATES OF MATTER EXERCISE - ADDITIONAL PRACTICE EXERCISE -PRACTICE SHEET (ADVANCED) (LINKED COMPREHENSION TYPE QUESTIONS) (PASSAGE- IV)2videos
STATES OF MATTER
- BOOK - AAKASH SERIESCHAPTER - SURFACE CHEMISTRYEXERCISE - Objective Excersice - 4 (ASSERTION (A)& REASON (R ) TYPE QUESTION)34videos
SURFACE CHEMISTRY
Similar Questions
Combustion of 2.24 its ethane at STP requires
03:49View Solution10 moles of SO2 and 4 moles of O2 are mixed in a closed vessel of volume 2 litres. The mixture is heated in the presence of Pt catalyst. Following reaction takes place:
2SO2(g)+O2(g)→2SO3(g)
Assuming the reaction proceeds to completion.
Select the correct statement.View SolutionThe oxidation number of iron in brown ring complexes +x. What is value of x.
03:17View SolutionAt a particular temperature and pressure for a real gas Van der Waal's equation can be written as:
(P+aV2m)(Vm−b)=RT
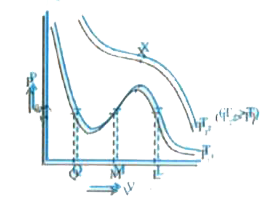
where Vm is molar volume of gas. This is cubic equation in the variable Vm and therefore for any single value of P & T there should be 3 values of Vm. Which are shown in graph as Q, M and L.
As temperature is made to increase at a certain higher temperature the three values of Vm becomes identical. The temperature, pressure & molar volume at point X are called Tc, Pc & Vc for real gas. The compressibility factor in terms of Pc, Vc and T is called Zc.
The expression of Van dcr Waal's constant 'a' can be given asView Solution(A) De-emulsification is a reverse process of emulsion formation
(R ) During de-emulsification , the emulsion breaks to give oil and water.03:21View SolutionA 5.0mL of solution of H2O2 liberates 0.508g of iodine from acidified KI solution. Calculate the strength of H2O2 solution in terms of volume strength at STP.
01:56View SolutionStrength of the sample of H_(2)O_(2) is generally expressed in terms of volume strength . It means the volume of oxygen liberated at NTP by heating one volume of H_(2)O_(2) . The concentration of H_(2)O_(2) in a solution can also expressed as percentage of H_(2)O_(2) in solution . Normality of this solution can be calculated if the equivalent mass of H_(2) O_(2) is known . Percentage strength of the above H_(2)O_(2) solution is
03:49View Solution10mL of a solution of H_(2)O_(2) liberated 0.5 g of iodine from Kl solution. The percentage of H_(2)O_(2) in the solution is:
View Solution17 g of H_(2)O_(2) solution on heating gave 1120 mL of O_(2) at 1 atm and 273 K. The percentage by weight of H_(2)O_(2) is
03:49View SolutionWhat is the percentage strength of a solution of 100 volume H_(2)O_(2) ?
View SolutionThe strength of H_(2)O_(2) (in g/litre) in 11.2 volume solution of H_(2)O_(2) is
04:16View SolutionA 5.0 cm^(3) solution of H_(2)O_(2) liberates 0.508 g of iodine from an acidified KI solution. Calculate the strength of H_(2)O_(2) solution in terms of volume strength of STP.
01:40View SolutionThe strength of H2O2 (in g/l ) in 11.2 volume solution of H2O2 is
01:40View SolutionA 5.0mL of solution of H2O2 liberates 0.508g of iodine from acidified KI solution. Calculate the strength of H2O2 solution in terms of volume strength at STP.
01:40View SolutionPercentage strength of the above H_(2)O_(2) solution is :
01:40View Solution

