Density of gas is inversely proportional to absolute temperature and directly proportional to pressure
= constant
Density at a particular temperature and pressure can be calculated bousing ideal gas equation
The density of at 1 atm and 273K isSolution in Telugu
Step by step video & image solution for Density of gas is inversely proportional to absolute temperature and directly proportional to pressure rArr d prop P/T rArr (dT)/P = constant rArr (d_(1)T_(1))/P_(1) =(d_(2)T_(2))/P_(2) Density at a particular temperature and pressure can be calculated bousing ideal gas equation PV = nRT rArr PV = ("mass")/("molar mass (M)") x RT P xx M =("mass")/("volume") xx RT rArr P xx M = d xx RT d=(PM)/(RT) The density of at 1 atm and 273K is by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- STATES OF MATTER BOOK - AAKASH SERIESCHAPTER - STATES OF MATTER EXERCISE - ADDITIONAL PRACTICE EXERCISE -PRACTICE SHEET (ADVANCED) (LINKED COMPREHENSION TYPE QUESTIONS) (PASSAGE- IV)
2 Videos
- STATES OF MATTER BOOK - AAKASH SERIESCHAPTER - STATES OF MATTER EXERCISE - ADDITIONAL PRACTICE EXERCISE- PRACTICE SHEET (ADVANCED) (LINKED COMPREHENSION TYPE QUESTIONS) (PASSAGE- II)
2 Videos
- SOLUTIONS BOOK - AAKASH SERIESCHAPTER - SOLUTIONS EXERCISE - Objective Exercise -4
50 Videos
- STOICHIOMETRYBOOK - AAKASH SERIESCHAPTER - STOICHIOMETRYEXERCISE - PRACTICE SHEET (ADVANCED) (INTEGER TYPE QUESTION)
2 Videos
Similar Questions
At a particular temperature and pressure for a real gas Van der Waal's equation can be written as:
(P+aV2m)(Vm−b)=RT
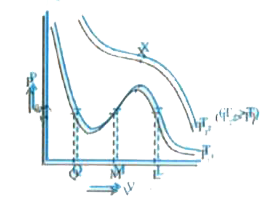
where Vm is molar volume of gas. This is cubic equation in the variable Vm and therefore for any single value of P & T there should be 3 values of Vm. Which are shown in graph as Q, M and L.
As temperature is made to increase at a certain higher temperature the three values of Vm becomes identical. The temperature, pressure & molar volume at point X are called Tc, Pc & Vc for real gas. The compressibility factor in terms of Pc, Vc and T is called Zc.
The expression of Van dcr Waal's constant 'a' can be given as
View SolutionThe intermolecular forces operating between two constituent particles depends on the distance between the centres of the molecules. Dipole-dipole interactions are inversely proportional to 3rd power of the distance where as dipole induced dipole interaction are inversely proportional to the sixth power of intermolecular distances.
The forces in dry ice are proportional to (r = intermolecular distance)
View SolutionAssertion : Molarity of a solution decreases with an increase of temperature
Reason : As temperature increases volume of the solution increases.
View SolutionAmmonia is oxised by oxygen to give nitric oxide and water. The weight of water produced per gram of nitric oxide is 0.1×xg. What is value of d.
View SolutionUsing the equation of state pV=nRT , show that at a given temperature the density of gas is proportional to gas pressure p .
View SolutionIf P, V, M, T and R are symbols of pressure, volume, molecular weight, temperature and Gas contstant, what is the equation of density of ideal gas
View SolutionUsing the equation of state pV=nRT, show that at a given temperature the density of gas is proportional to gas pressure p.
View SolutionUsingg the equation of state PV=nRT, show that at a given temperature, density of a gas is proportional to the gas pressure P.
View SolutionThe density of gas A is dA at a temperature of TAK, and the density of gas B is dB at a temperature of TBK. The molar mass of A is 4 times that of B. if TA:TB=2:1 and dA,dB=1:2, the ratio of pressure of A to B is-
View SolutionUsing the equation of state pV=nRT, show that at a given temperature density of a gas is proportional to gas pressure p.
View SolutionFor the gas equation P = ( RT )/( V - b) - ( a)/( TV^(2)) , following conclusions are found true ( 1) lim ( RT - PV ) = 0, P rarr alpha, T rarr beta ( 2) lim (V) /( T ) = ( R )/( P ) , T rarr gamma Which is the correct set of the vlaues of alpha, beta and gamma ?
View SolutionUsing the equation of state pV= nRT show that at a given temperature, the density of the gas is proportion a to gas the gas pressure P.
View SolutionDensity of gas is inversely proportional to absolute temperature and directly proportional to pressure rArr d prop P/T rArr (dT)/P = constant rArr (d_(1)T_(1))/P_(1) =(d_(2)T_(2))/P_(2) Density at a particular temperature and pressure can be calculated bousing ideal gas equation PV = nRT rArr PV = ("mass")/("molar mass (M)") x RT P xx M =("mass")/("volume") xx RT rArr P xx M = d xx RT d=(PM)/(RT) Which of the following has maximum density?
View SolutionDensity of gas is inversely proportional to absolute temperature and directly proportional to pressure rArr d prop P/T rArr (dT)/P = constant rArr (d_(1)T_(1))/P_(1) =(d_(2)T_(2))/P_(2) Density at a particular temperature and pressure can be calculated bousing ideal gas equation PV = nRT rArr PV = ("mass")/("molar mass (M)") x RT P xx M =("mass")/("volume") xx RT rArr P xx M = d xx RT d=(PM)/(RT) The density of gas is 3.8 g L^(-1) at STP. The density at 27°C and 700 mm Hg pressure will be
View SolutionUsing the equation of state pV=nRT, show that at a given temperature the density of gas is proportional to gas pressure p.
View Solution
