Let the line x−8y+k=0, k∈l meets the rectangular hyperbola xy=1 at the points whose abscissae are integers then the number of such lines is
Step by step video & image solution for Let the line x-8y+k=0, k in l meets the rectangular hyperbola xy=1 at the points whose abscissae are integers then the number of such lines is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
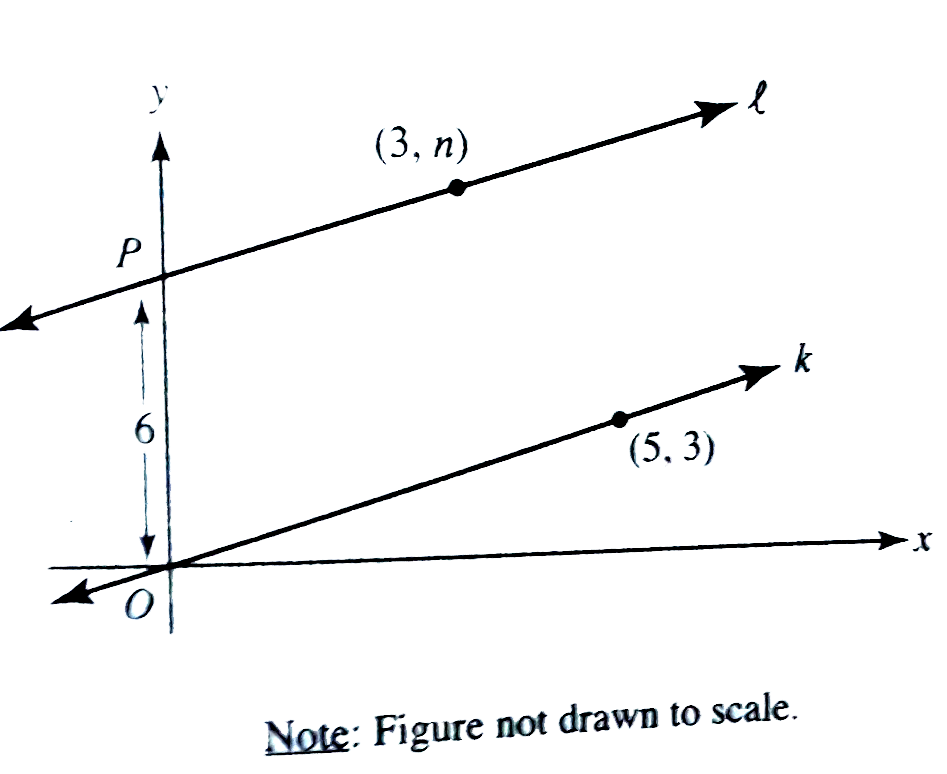
In the xy-coordinate system shown above , the lines l and k are parallel , and distance OP is 6. if the points (5,3) is on line k , and the point (3,n) is on line l. what is the value of n ?
View SolutionIF the line x+y+k=0 is a normal to the hyperbola x29−y24=1 then k=
View SolutionIF the line x+y+k=0 is a normal to the hyperbola x29−y24=1 then k=
View Solutionk≤0 के लिए, रेखा y=x, y=kex पर मिलती है [
View SolutionThe number of values of k for which the lines (k+1)x+8y=4kandkx+(k+3)y=3k−1 are coincident is __________
View SolutionThe number of values of k for which the lines (k+1)x+8y=4kandkx+(k+3)y=3k−1 are coincident is __________
View Solutionआयतिय अतिपरवलय xy=k2, जिसका केंद्र C है, पर किसी बिंदु P पर खींची गयी स्पर्श रेखा निर्देशक अंक्षो को Q तथा R पर मिलती हो, तो त्रिभुज CQR के परिकेन्द्र का बिन्दुपथ है-
View SolutionProve that the locus of the point of intersection of the lines sqrt3 x -y -4 sqrt3 k =0 and sqrt3 k x+ ky - 4 sqrt3 =0, for different values of k, is a hyperbola whose eccentricity is 2.
View Solution
