Question

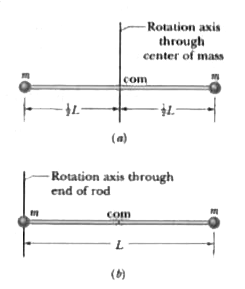
Figure a rigid body consisting of two particles of mass m connected by a rod of length L and negligible mass.
(a) What is the rotational inertia $I_{com}$ about an axis through the center of mass, perpendicular to the rod as shown?
(b) What is the rotational inertia I of the body about an axis through the left end of the rod and parallel to the first axis.

Explanation

(a) Because we have only two particles with mass, we can find the body.s rotational inertia `I_(com)` by using Eq. rather than by integration. That is, we find the rotational inertia of each particle and then just add the results.
Calculations: For the two particles, each at perpendicular distance 1/2 L from the rotation axis, we have
`I=summ_(i)r_(i)^(2)=(m)(1/2L)^(2)+(m)(1/2L)^(2)`
= `1/2mL^(2)`
(b) This situation is simple enough that we can find I using either of two techniques. The first is similar to the one used in part (a). The other, more powerful one is to apply the parallel-axis theorem.
Calculation method : We calculate I as in part (a), except here the perpendicular distance `r_(i)` is zero for the particle on the left and L for the particle on the right.
`I=m(0)^(2)+mL^(2)=mL^(2)`.