In Fig., three forces, each of magnitude 2.0 N, act on a particle. The particle is in the xz' plane at point A given by position vector $\to r$ , where r = 3.0 m and $θ = 30^{\circ}$ . What is the torque, about the origin O, due to each force?

Text Solution

Verified by Experts

Because the three force vectors do not lie in a plane, we must use cross products, with magnitudes given by Eq. $(τ = r F sin ϕ)$ and direction given by the right-hand rule.
Calculations: Because we want the torque with respect to the origin O, the vector $\to r$ required for each cross product is the given position vector. To determine the angle $ϕ$ between $\to r$ and each force, we shift the force vectors of Fig. each in turn, so that their tails are at the origin. Fig., c, and d, which are direct views of the xz plane, show the shifted force vectors ${\to F}_{1}, {\to F}_{2} and {\to F}_{3}$ ,

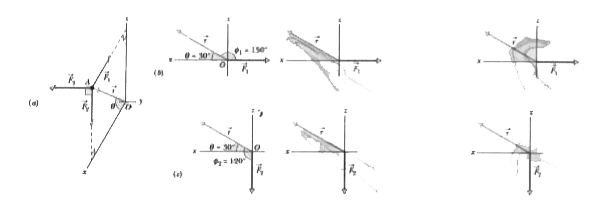
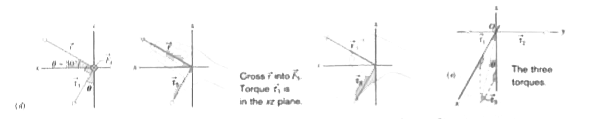
respectively. In the angle between the direction of $\to r$ and ${\to F}_{3} is 90^{\circ}$ and the symbol means ${\to F}_{3}$ is directed into the page.
$τ_{1} = r F_{1} {sin ϕ}_{1} = (3.0 m) (2.0 N) ({sin 150}^{\circ}) = 3.0 N \cdot m$ ,
$τ_{2} = r F_{2} {sin ϕ}_{2} = (3.0 m) (2.0 N) ({sin 120}^{\circ}) = 5.2 N \cdot m$
and $τ_{3} = r F_{3} {sin ϕ}_{3} = (3.0 m) (2.0 N) ({sin 90}^{\circ}) = 6.0 N \cdot m$ .

Updated on:21/07/2023

The force $7 ˆ i + 3 ˆ j - 5 ˆ k$ acts on a particle whose position vector is $ˆ i - ˆ j + ˆ k$ . What is the torque of a given force about the origin ?
A $2 ˆ i + 12 ˆ j + 10 ˆ k$
B $2 ˆ i + 10 ˆ j + 12 ˆ k$
C $2 ˆ i + 10 ˆ j + 10 ˆ k$
D $10 ˆ i + 2 ˆ j + ˆ k$
If $\to F$ is the force acting in a particle having position vector $\to r$ and $\to τ$ be the torque of this force about the origin, then
A $\to r . \to τ \neq 0 and \to F . \to τ = 0$
B $\to r . \to τ > 0 and \to F . \to τ < 0$
C $\to r . \to τ = 0 and \to F . \to τ = 0$
D $\to r . \to τ = 0 and \to F . \to τ \neq 0$
Let $\to F$ be the force acting on a particle having position vector $\to r$ and $\to τ$ be the torque of this force about the origin. Then
A $\to r . \to τ \neq 0 and \to F . \to τ \neq 0$
B $\to r . \to τ = \neq 0 and \to F . \to τ = 0$
C $\to r . \to τ = \neq 0 and \to F . \to τ \neq 0$
D $\to r . \to τ = 0 and \to F . \to τ = 0$