To throw an 80 kg opponent with a basic judo hip throw, you intend to pull his uniform with a force $\to F$ and a moment arm $d_{1}$ = 0.30 m from a pivot point on your right hip. You wish to rotate him about the pivot point with an angular acceleration $α of - 6.0 r a d / s^{2}$ - that is, with an angular acceleration that is clockwise in the figure. Assume that his rotational inertia I relative to the pivot point is $15 k g \cdot m^{2}$ .
(a) What must the magnitude of $\to F$ be if, before you throw him, you benf your opponent forward to bring his center of mass to your hip?
(b) What must the magnitude of $\to F$ be if your opponent remains upright before you throw him, so that ${\to F}_{g}$ has a moment arm $d_{2} = 0.12 m$ ?

Text Solution

Verified by Experts

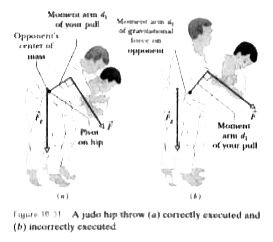
(a) We can relate your pull $\to F$ on your opponent to the given angular acceleration $α$ via Newton.s second law for rotation $(τ_{net} = I α)$ .
Calculations: As his feet leave the floor, we can assume that only three forces act on him: your pull $\to F$ , a force $\to N$ on him from you at the pivot point, and the gravitational force ${\to F}_{g}$ . To use $τ_{net} = I α$ , we need the corresponding three torques, each about the pivot point.
From Eq. $(τ = r_{⊥} F)$ , the torque due to your pull $\to F$ is equal to $- d_{1} F$ , where $d_{1}$ is the moment arm $r_{⊥}$ and the sign indicates the clockwise rotation this torque tends to cause. The torque due to $\to N$ is zero, because $\to N$ acts at the pivot point and thus has moment arm $r_{⊥} = 0$ .
To evaluate the torque dur ${\to F}_{g}$ , we can assume that ${\to F}_{g}$ acts at your opponent.s center of mass. With the center of mass at the pivot point, ${\to F}_{g}$ has moment arm $r_{⊥} = 0$ and thus the torque dur to ${\to F}_{g}$ is zero. So, the only torque on your opponent is due to your pull $\to F$ , and we can write $τ_{net} = I α$ as
$- d_{1} F = I α$
We then find
$F = \frac{- I α}{d_{1}} = \frac{- (15 k g \cdot m^{2}) (- 6.0 r a d / s^{2})}{0.30 m}$
= 300 N.
(b) Because the moment arm for ${\to F}_{g}$ is no longer zero, the torque due to ${\to F}_{g}$ is now equal to $d_{2} m g$ and is positive because the torque attempts counterclockwise rotation.
Calculations: Now we write $τ_{net} = I α$ as
$- d_{1} F + d_{2} m g = I α$
$F = - \frac{I α}{d_{1}} + \frac{d_{2} m g}{d_{1}}$ .
From (a), we know that the first term on the right is equal to 300 N. Substituting this and the given data, we have
$F = 300 N + \frac{(0.12 m) (80 k g) (9.8 m / s^{2})}{0.30 m}$
= $613.6 N \approx 610 N$ .

Updated on:21/07/2023

A circular disk of radius 2.0 m rotates, starting from rest, with a constant angular acceleration of $20.0 r a d / s^{2}$ . What is the tangential acceleration of a point on the edge of the disk at the instant that its angular speed is 1.0 rev/s?
A $40 m / s^{2}$
B $110 m / s^{2}$
C $79 m / s^{2}$
D $120 m / s^{2}$
A body rotates about a fixed axis with an angular acceleration of $3 r a d / s^{2}$ The angle rotated by it during the time when its angular velocity increases frm 10 rad/s to 20 rad/s (in radian) is
A50
B100
C150
D200
A wheel has angular acceleration of $3.0 r a d / s^{2}$ and an initial angular speed of $2.00 r a d / s$ , In a time of 2 s it has rotated through an angle (in radian) of
A6
B10
C12
D4